题目内容
求满足cos(πsinx)=
解析:cos(πsinx)=![]() ,又πsinx∈(-π,π),
,又πsinx∈(-π,π),
当πsinx∈[0,π]时,πsinx=arccos![]() =
=![]() ,sinx=
,sinx=![]() .
.
x=arcsin![]() 或π-arcsin
或π-arcsin![]() .
.
当πsinx∈[-π,0]时,
πsinx=-arccos![]() =-
=-![]() ,sinx=-
,sinx=-![]() .
.
∴x=-arcsin(-![]() )+π或2π+arcsin(-
)+π或2π+arcsin(-![]() ).
).
因此,所求角x的集合为{arcsin![]() ,π-arcsin
,π-arcsin![]() ,π-arcsin(-
,π-arcsin(-![]() ),2π+arcsin(-
),2π+arcsin(-![]() )}.
)}.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
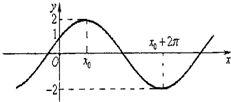 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<