题目内容

已知不等式2x-1＞m(x2-1)(m≠0).

(1)若对于所有实数x不等式恒成立,求m的取值范围;?

(2)若对于m∈［-2,2］不等式恒成立,求实数x的取值范围.

解:(1)原不等式等价于mx2-2x+(1-m)＜0对x∈R成立.当且仅当解得m∈.

(2)设f(m)=(x2-1)m-(2x-1).?

由于m∈［-2,2］时,f(m)＜0恒成立.?

当且仅当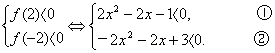

解①得＜x＜,?

解②得x＜或x＞,所以得＜x＜,?

即所求x的范围是{x|＜x＜}.

练习册系列答案
相关题目
已知不等式2x-1＞m（x2-1）．
（1）若对于所有实数x，不等式恒成立，求m的取值范围；
（2）若对于m∈[-2，2]不等式恒成立，求x的取值范围．
若已知不等式2x-1＞m（x2-1）对满足|m|≤2的一切实数m的取值都成立，则x的取值范围为
 
．
已知不等式2x-1＞m（x2-1）对于m∈[0，1]恒成立，则实数x的取值范围为
(
1
2
，2)
(
1
2
，2)
．
已知不等式2x-1＞m（x2-1）对一切|m|≤2恒成立，则实数x的取值范围是
（
-1+
7
2
，
1+
3
2
）
（
-1+
7
2
，
1+
3
2
）
．
已知不等式
2x+1
＞1的解集为A，不等式x2-（2+a）x+2a＜0的解集为B．
（1）求集合A及B；    （2）若A⊆B，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网