题目内容
【题目】已知函数f(x)=lnx+mx(m为常数).
(1)讨论函数f(x)的单调区间;
(2)当 ![]() 时,设
时,设 ![]() 的两个极值点x1 , x2(x1<x2)恰为h(x)=2lnx﹣ax﹣x2的零点,求
的两个极值点x1 , x2(x1<x2)恰为h(x)=2lnx﹣ax﹣x2的零点,求 ![]() 的最小值.
的最小值.
【答案】
(1)解: ![]() ,x>0,
,x>0,
当m<0时,由1+mx>0,解得 ![]() ,
,
即当 ![]() 时,f'(x)>0,f(x)单调递增;
时,f'(x)>0,f(x)单调递增;
由1+mx<0解得 ![]() ,即当
,即当 ![]() 时,f'(x)<0,f(x)单调递减;
时,f'(x)<0,f(x)单调递减;
当m=0时, ![]() ,即f(x)在(0,+∞)上单调递增;
,即f(x)在(0,+∞)上单调递增;
当m>0时,1+mx>0,故f'(x)>0,即f(x)在(0,+∞)上单调递增.
所以当m<0时,f(x)的单调递增区间为 ![]() ,单调递减区间为
,单调递减区间为 ![]() ;
;
当m≥0时,f(x)的单调递增区间为(0,+∞)
(2)解:由 ![]() 得
得 ![]() ,
,
由已知x2+mx+1=0有两个互异实根x1,x2,
由根与系数的关系得x1+x2=﹣m,x1x2=1,
因为x1,x2(x1<x2)是h(x)的两个零点,
故 ![]() ①
① ![]() ②
②
由②﹣①得: ![]() ,
,
解得  ,
,
因为 ![]() ,得
,得 ![]() ,
,
将  代入得:
代入得:

=  =
=  ,
,
所以  ,
,
设 ![]() ,因为
,因为 ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ,所以t≥2.
,所以t≥2.
构造 ![]() ,得
,得 ![]() ,
,
则 ![]() 在[2,+∞)上是增函数,
在[2,+∞)上是增函数,
所以 ![]() ,即
,即 ![]() 的最小值为
的最小值为 ![]()
【解析】(1)求出函数的导数,通过讨论m的范围,求出函数的单调区间即可;(2)求出函数的导数,得到x1+x2=﹣m,x1x2=1,求出 ![]() 的解析式,根据函数的单调性求出其最小值即可.
的解析式,根据函数的单调性求出其最小值即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:
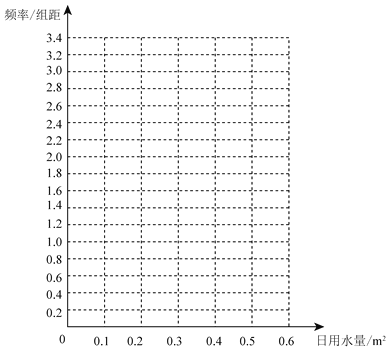
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
