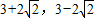题目内容
已知函数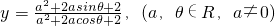 .那么对于任意的a,θ,函数y的最大值与最小值分别为
.那么对于任意的a,θ,函数y的最大值与最小值分别为
- A.
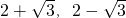
- B.
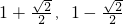
- C.
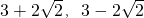
- D.3,1
A
分析:把已知函数转化为关于cosθ,sinθ的方程,利用直线与圆的位置关系,求出y的范围即可得到选项.
解答:设 ,则2atcosθ-2asinθ+(t-1)(a2+2)=0,
,则2atcosθ-2asinθ+(t-1)(a2+2)=0,
所以直线2atx-2ay+(t-1)(a2+2)=0与圆x2+y2=1有公共点,
从而有
得
于是 ,
,
即t2-4t+1≤0
得 ;
;
故选A.
点评:本题考查直线与圆的位置关系,考查转化思想的应用,构造直线与圆的位置关系是解题的关键.
分析:把已知函数转化为关于cosθ,sinθ的方程,利用直线与圆的位置关系,求出y的范围即可得到选项.
解答:设
 ,则2atcosθ-2asinθ+(t-1)(a2+2)=0,
,则2atcosθ-2asinθ+(t-1)(a2+2)=0,所以直线2atx-2ay+(t-1)(a2+2)=0与圆x2+y2=1有公共点,
从而有

得

于是
 ,
,即t2-4t+1≤0
得
 ;
;故选A.
点评:本题考查直线与圆的位置关系,考查转化思想的应用,构造直线与圆的位置关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
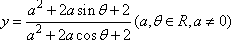 ,那么对于任意的a,
,那么对于任意的a,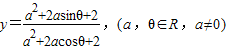 .那么对于任意的a,θ,函数y的最大值与最小值分别为 ( )
.那么对于任意的a,θ,函数y的最大值与最小值分别为 ( )