题目内容
设二次函数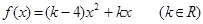 ,对任意实数
,对任意实数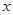 ,有
,有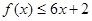 恒成立;数列
恒成立;数列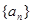 满足
满足 .
.
(1)求函数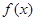 的解析式和值域;
的解析式和值域;
(2)证明:当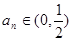 时,数列
时,数列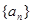 在该区间上是递增数列;
在该区间上是递增数列;
(3)已知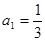 ,是否存在非零整数
,是否存在非零整数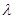 ,使得对任意
,使得对任意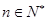 ,都有
,都有
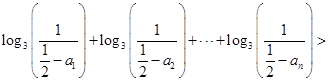
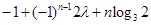 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.
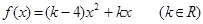 ,对任意实数
,对任意实数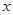 ,有
,有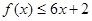 恒成立;数列
恒成立;数列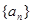 满足
满足 .
.(1)求函数
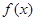 的解析式和值域;
的解析式和值域;(2)证明:当
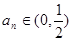 时,数列
时,数列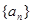 在该区间上是递增数列;
在该区间上是递增数列;(3)已知
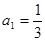 ,是否存在非零整数
,是否存在非零整数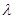 ,使得对任意
,使得对任意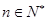 ,都有
,都有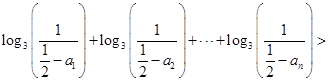
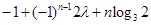 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.(1)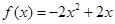 ,值域为
,值域为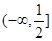 ;(2)证明见解析;(3)存在,且
;(2)证明见解析;(3)存在,且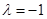 .
.
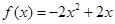 ,值域为
,值域为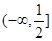 ;(2)证明见解析;(3)存在,且
;(2)证明见解析;(3)存在,且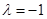 .
.试题分析:(1)这是一个不等式恒成立问题,把不等式转化为
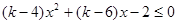 恒成立,那么这一定是二次不等式,恒成立的条件是
恒成立,那么这一定是二次不等式,恒成立的条件是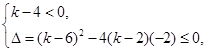 可解得
可解得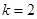 ,从而得到
,从而得到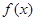 的解析式,其值域也易求得;(2)要证明数列
的解析式,其值域也易求得;(2)要证明数列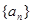 在该区间上是递增数列,即证
在该区间上是递增数列,即证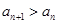 ,也即
,也即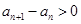 ,根据
,根据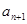 的定义,可把
的定义,可把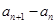 化为关于
化为关于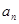 的二次函数,再利用
的二次函数,再利用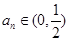 ,可得结论
,可得结论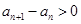 ;(3)这是一道存在性问题,解决问题的方法一般是假设存在符合题意的结论,本题中假设
;(3)这是一道存在性问题,解决问题的方法一般是假设存在符合题意的结论,本题中假设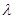 存在,使不等式成立,为了求出
存在,使不等式成立,为了求出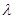 ,一般要把不等式左边的和求出来,这就要求我们要研究清楚第一项是什么?这个和是什么数列的和?由
,一般要把不等式左边的和求出来,这就要求我们要研究清楚第一项是什么?这个和是什么数列的和?由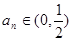 ,从而
,从而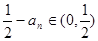 ,
,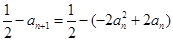
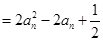
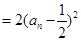 ,不妨设
,不妨设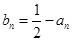 ,则
,则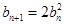 (
(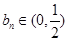 ),对这个递推公式我们可以两边取对数把问题转化为
),对这个递推公式我们可以两边取对数把问题转化为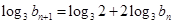 ,这是数列
,这是数列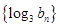 的递推公式,可以变为一个等比数列,方法是上式可变为
的递推公式,可以变为一个等比数列,方法是上式可变为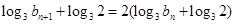 ,即数列
,即数列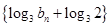 是公比为2的等比数列,其通项公式易求,反过来,可求得
是公比为2的等比数列,其通项公式易求,反过来,可求得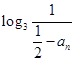 ,从而求出不等式左边的和,化简不等式.
,从而求出不等式左边的和,化简不等式.试题解析:(1)由
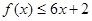 恒成立等价于
恒成立等价于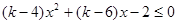 恒成立,
恒成立, 从而得:
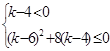 ,化简得
,化简得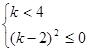 ,从而得
,从而得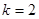 ,所以
,所以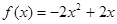 ,
,3分
其值域为
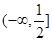 . 4分
. 4分(2)解:
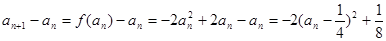
6分
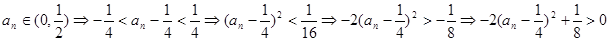 , 8分
, 8分从而得
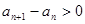 ,即
,即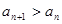 ,所以数列
,所以数列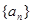 在区间
在区间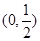 上是递增数列. 10分
上是递增数列. 10分(3)由(2)知
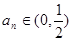 ,从而
,从而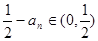 ;
;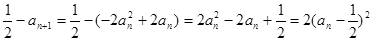 ,即
,即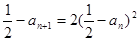 ;
;12分
令
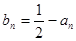 ,则有
,则有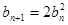 且
且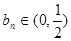 ;
;从而有
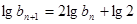 ,可得
,可得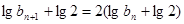 ,所以数列
,所以数列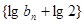 是
是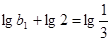 为首项,公比为
为首项,公比为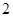 的等比数列,
的等比数列,从而得
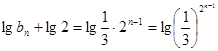 ,即
,即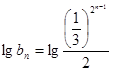 ,
,所以
 ,
,所以
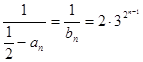 ,所以
,所以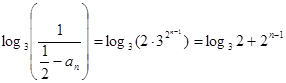 ,
,所以,
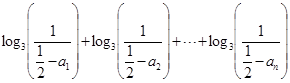
 .
.即
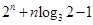
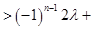
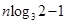 ,所以,
,所以,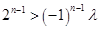 恒成立. 15分
恒成立. 15分当
 为奇数时,即
为奇数时,即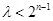 恒成立,当且仅当
恒成立,当且仅当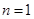 时,
时,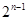 有最小值
有最小值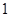 为.
为.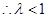 16分
16分当
 为偶数时,即
为偶数时,即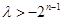 恒成立,当且仅当
恒成立,当且仅当 时,有最大值
时,有最大值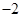 为.
为. 17分
17分所以,对任意
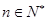 ,有
,有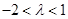 .又
.又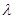 非零整数,
非零整数,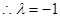 18分
18分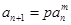 ,
,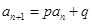 的数列通项公式,等比数列的前
的数列通项公式,等比数列的前 项和.
项和.
练习册系列答案
相关题目
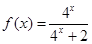
 ,求
,求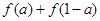 的值;
的值;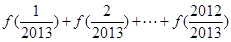 的值.
的值.
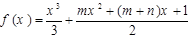 的两个极值点分别为
的两个极值点分别为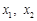 ,且
,且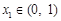 ,
,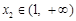 ,点
,点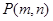 表示的平面区域为
表示的平面区域为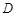 ,若函数
,若函数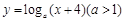 的图像上存在区域
的图像上存在区域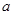 的取值范围是( )
的取值范围是( )



 与该班人数
与该班人数 之间的函数关系用取整函数
之间的函数关系用取整函数 (
( 表示不大于
表示不大于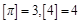 )可表示为( )
)可表示为( )



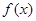 满足
满足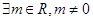 ,对定义域内的任意
,对定义域内的任意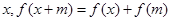 恒成立,则称
恒成立,则称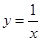 ; ②
; ②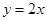 ; ③
; ③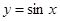 ; ④
; ④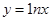
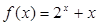 ,
, 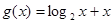 ,
,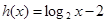 的零点分别是
的零点分别是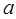 ,
,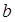 ,
,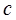 。则( )
。则( ) <
< <
<
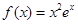 既无最小值也无最大值;
既无最小值也无最大值;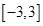 上随机取一个数
上随机取一个数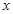 ,使得
,使得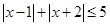 成立的概率为
成立的概率为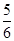 ;
;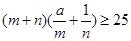 对任意正实数
对任意正实数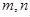 恒成立,则正实数
恒成立,则正实数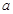 的最小值为16;
的最小值为16;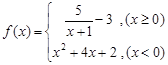 ,若方程
,若方程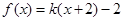 恰有三个不同的实根,则实数
恰有三个不同的实根,则实数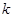 的取值范围是
的取值范围是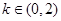 ;以上正确的命题序号是:_______.
;以上正确的命题序号是:_______. 满足对任意的
满足对任意的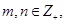 都有
都有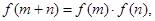 且
且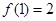 ,则
,则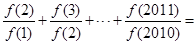 ( )
( )