题目内容
若函数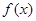 满足
满足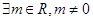 ,对定义域内的任意
,对定义域内的任意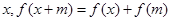 恒成立,则称
恒成立,则称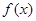 为m函数,现给出下列函数:
为m函数,现给出下列函数:
①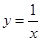 ; ②
; ②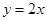 ; ③
; ③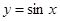 ; ④
; ④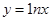
其中为m函数的序号是 .(把你认为所有正确的序号都填上)
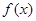 满足
满足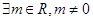 ,对定义域内的任意
,对定义域内的任意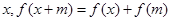 恒成立,则称
恒成立,则称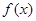 为m函数,现给出下列函数:
为m函数,现给出下列函数:①
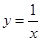 ; ②
; ②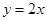 ; ③
; ③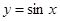 ; ④
; ④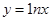
其中为m函数的序号是 .(把你认为所有正确的序号都填上)
②③
试题分析:①若
 ,则由
,则由 得
得 ,即
,即 ,所以不存在常数
,所以不存在常数 使
使 成立,所以①不是m函数。②若
成立,所以①不是m函数。②若 ,由
,由 得,
得, ,此时恒成立,所以②
,此时恒成立,所以②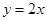 是m函数。③若
是m函数。③若 ,由
,由 得
得 ,所以当
,所以当 时,
时, 成立,所以③
成立,所以③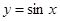 是m函数。④若
是m函数。④若 ,则由
,则由 得
得 ,即
,即 ,所以
,所以 ,要使
,要使 成立则有
成立则有 ,所以方程无解,所以④
,所以方程无解,所以④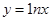 不是m函数。所以为m函数的序号是②③。
不是m函数。所以为m函数的序号是②③。
练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 .
. 的值;
的值; 在
在 上是减函数.
上是减函数. 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元; 元的超额费.
元的超额费. (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
 的值.
的值.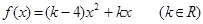 ,对任意实数
,对任意实数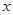 ,有
,有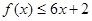 恒成立;数列
恒成立;数列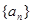 满足
满足 .
.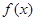 的解析式和值域;
的解析式和值域;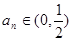 时,数列
时,数列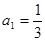 ,是否存在非零整数
,是否存在非零整数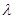 ,使得对任意
,使得对任意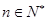 ,都有
,都有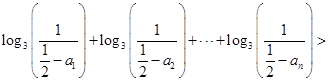
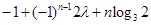 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由. 有两个不同的零点,则实数
有两个不同的零点,则实数 的取值范围是( )
的取值范围是( )





 且
且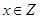 ),则
),则 的值域是 ( )
的值域是 ( )



 的图像,它与x轴有4个不同的公共点.给出下列四个区间,不能用二分法求出函数
的图像,它与x轴有4个不同的公共点.给出下列四个区间,不能用二分法求出函数




 ,若
,若 在区间
在区间 上恒有解,则
上恒有解,则 的取值范围为 .
的取值范围为 . )上的函数
)上的函数 是它的导函数,且恒有
是它的导函数,且恒有 成立,则( )
成立,则( )


