题目内容
以下四个命题:
①函数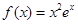 既无最小值也无最大值;
既无最小值也无最大值;
②在区间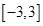 上随机取一个数
上随机取一个数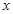 ,使得
,使得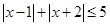 成立的概率为
成立的概率为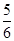 ;
;
③若不等式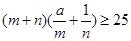 对任意正实数
对任意正实数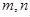 恒成立,则正实数
恒成立,则正实数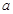 的最小值为16;
的最小值为16;
④已知函数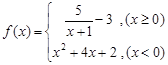 ,若方程
,若方程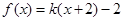 恰有三个不同的实根,则实数
恰有三个不同的实根,则实数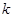 的取值范围是
的取值范围是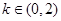 ;以上正确的命题序号是:_______.
;以上正确的命题序号是:_______.
①函数
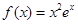 既无最小值也无最大值;
既无最小值也无最大值;②在区间
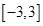 上随机取一个数
上随机取一个数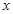 ,使得
,使得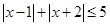 成立的概率为
成立的概率为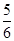 ;
;③若不等式
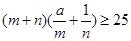 对任意正实数
对任意正实数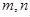 恒成立,则正实数
恒成立,则正实数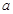 的最小值为16;
的最小值为16;④已知函数
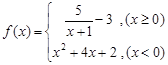 ,若方程
,若方程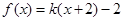 恰有三个不同的实根,则实数
恰有三个不同的实根,则实数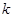 的取值范围是
的取值范围是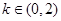 ;以上正确的命题序号是:_______.
;以上正确的命题序号是:_______.②③
试题分析:对①,函数
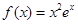 显然有最小值
显然有最小值 ,故错.
,故错.对②,
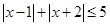 的解为
的解为 ,由几何概型的概率公式得,概率为
,由几何概型的概率公式得,概率为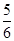 ,正确.
,正确.对③,
 .不等式
.不等式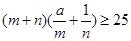 对任意正实数
对任意正实数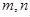 恒成立,则
恒成立,则 ,成立.
,成立.④作出
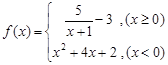 的图象如图所示.直线
的图象如图所示.直线 恒过点
恒过点 ,该点恰为抛物线
,该点恰为抛物线 的顶点.
的顶点.
由图可得,要有三个不同的交点,斜率
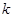 的取值范围为
的取值范围为

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
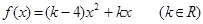 ,对任意实数
,对任意实数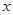 ,有
,有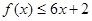 恒成立;数列
恒成立;数列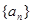 满足
满足 .
.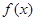 的解析式和值域;
的解析式和值域;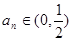 时,数列
时,数列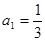 ,是否存在非零整数
,是否存在非零整数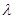 ,使得对任意
,使得对任意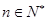 ,都有
,都有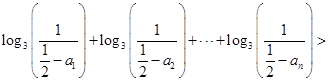
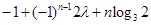 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.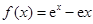 .
.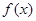 的最小值;
的最小值;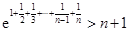
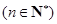 ;
;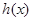 与
与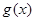 定义域上的任意实数
定义域上的任意实数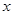 ,若存在常数
,若存在常数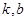 ,使得
,使得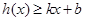 和
和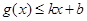 都成立,则称直线
都成立,则称直线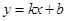 为函数
为函数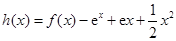 ,
,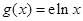 ,
, 和
和 ,定义运算“*”:
,定义运算“*”:  设
设 ,且关于
,且关于 的方程为
的方程为 恰有三个互不相等的实数根
恰有三个互不相等的实数根 、
、 、
、 ,则
,则 的取值范围是( )
的取值范围是( )



 ,若
,若 在区间
在区间 上恒有解,则
上恒有解,则 的取值范围为 .
的取值范围为 .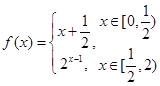 ,若存在
,若存在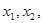 当
当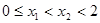 时,
时,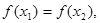 则
则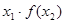 的取值范围是
的取值范围是 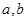 ,定义运算“
,定义运算“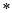 ”:
”: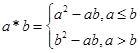 ,设
,设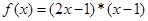 ,且关于x的方程
,且关于x的方程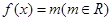 恰有三个互不相等的实数根
恰有三个互不相等的实数根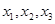 ,则
,则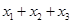 的取值范围是____________.
的取值范围是____________. ,若
,若 ,则
,则 .
.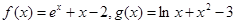 ,若实数
,若实数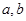 满足
满足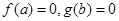 ,请将
,请将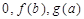 按从小到大的顺序排列 .(用“
按从小到大的顺序排列 .(用“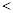 ”连接).
”连接).