题目内容
设△ABC的三内角
的对边长分别为a、b、c，已知a、b、c成等比数列，且
（Ⅰ）求角
的大小；
（Ⅱ）若
，求函数
的值域.
的对边长分别为a、b、c，已知a、b、c成等比数列，且（Ⅰ）求角
的大小；（Ⅱ）若
，求函数的值域. （Ⅰ）
（Ⅱ）
（Ⅱ）本试题主要是考查了解三角形和三角函数性质的运用。
（1）、因为a、b、c成等比数列以及正弦定理得到角B的值。
（2）根据三角函数中两角差的三角函数公式，得到关于x的单一函数，然后借助于值域得到结论。
解:（Ⅰ）因为a、b、c成等比数列，则
.由正弦定理得
.
又
，所以
.因为sinB＞0，则
.
因为B∈(0，π)，所以B＝
或
.
又，则
或
，即b不是△ABC的最大边，故. 
6分
（Ⅱ）因为，则
. 10分
，则
，所以
.
故函数
的值域是.
（1）、因为a、b、c成等比数列以及正弦定理得到角B的值。
（2）根据三角函数中两角差的三角函数公式，得到关于x的单一函数，然后借助于值域得到结论。
解:（Ⅰ）因为a、b、c成等比数列，则
.由正弦定理得. 又
，所以.因为sinB＞0，则. 因为B∈(0，π)，所以B＝
或.又
，则或，即b不是△ABC的最大边，故. 6分（Ⅱ）因为
，则. 10分，则，所以.故函数
的值域是. 
练习册系列答案
阅读快车系列答案
相关题目
的图像按向量
平移后所得函数图像的解析式为( ).
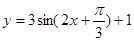
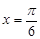是函数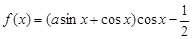
图象的一条对称轴．
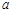的值；
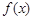在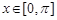
上的图象简图（不要求书写作图过程）．
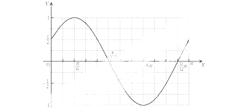
的导函数
的部分图像如图所示：图象与
轴交点
,与x轴正半轴的交点为A、C,B为图象的最低点 ,则函数
，
的最大值和最小正周期；
的内角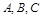
的对边分别
且
,
，若
求
的值．
时，求f(x)的值域. 
中,若
,求角
的大小.
的图象按向量
平移后,对应的函数为偶函数,求
取最小值时的向量
的图象向左平移
个单位，得到函数
的图象，则
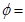
图象的一部分，则其函数解析式是（ ）
