Question

（文）椭圆

x2

a2

+

y2

b2

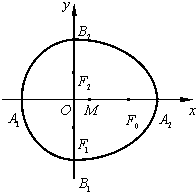
=1  (a＞b＞0)的焦点为F₁，F₂，若椭圆上有且仅有两点B₁，B₂满足∠F₁B₁F₂=∠F₁B₂F₂=120°，则a：b=

2

．

Answer 1

分析：先根据椭圆的对称性结合条件得出两点B₁，B₂必为椭圆的短轴的端点，再根据椭圆的对称性可知|B₁F₁|=|B₁F₂|，根据△F₁B₁F₂是等腰三角形可推断出短轴平分∠F₁B₁F₂，进而求得顶角的半角，进而根据sin60°=

|OF1|

|B1F1|

=

c

a

求得椭圆的a，c的关系，从而得出a：b．

解答：解：根据椭圆的对称性结合条件得出两点B₁，B₂必为椭圆的短轴的端点，
∵B₁是短轴的一个端点，
∴|B₁F₁|=|B₁F₂|
△F₁B₁F₂是等腰三角形
∴短轴平分∠F₁B₁F₂
∴顶角的一半是

120°

2

=60°
∴sin60°=

|OF1|

|B1F1|

=

c

a

（O为原点）
∴

c

a

=

3

2

⇒c=

3

2

a，
∴a：b=

a

a2-c2

=

a

a2-( 3 a 2 )2

=2
故答案为：2．

点评：本题主要考查了椭圆的应用，主要考查了椭圆的简单性质．此题关键是两点B₁，B₂必为椭圆的短轴的端点．