题目内容
已知A、B、C是△ABC的三个内角，a、b、c为其对应边，向量m＝(－1，
)，
n＝(cosA，sinA )，且 m·n＝1.
（1）求A；
（2）若 
＝(2,1 )， 
＝
，求△ABC的面积S.
[解析] (1)由m·n＝1，得sinA－cosA＝1，
(2)：由正弦定理，得＝＝
，
∴sinBcosC－cosBsinC＝0，即sin(B－C)＝0.
∵－π<B－C<π，∴B－C＝0，即B＝C.
又∵A＝
，∴△ABC为等边三角形．
∵c＝|
|＝
，∴S＝
×()2＝
.
练习册系列答案
阅读快车系列答案
相关题目
（
为虚数单位）等于 ，
cos6°－
sin6°，b＝2sin13°cos13°，c＝
，则( )
项和为
，且
，则数列{an}的通项公式
＝_____.
的定义域为（） 
的零点所在的大致区间是（）
则下列式子表示正确的个数为 （ ） 
①
; ②
; ③ 
;④
.
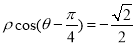，以极点为原点，极轴为x轴的非负半轴建立平面直角坐标系，曲线C2的参数方程为
，求曲线C1与曲线C2交点的直角坐标