题目内容
求函数f(x)=xex的单调区间和极值.
解:∵函数f(x)=xex的定义域为R,
f'(x)=(xex)′=x′ex+x(ex)′=ex+xex
令f'(x)=ex+xex=ex(1+x)=0,解得:x=-1.
列表:
由表可知函数f(x)=xex的单调递减区间为(-∞,-1),单调递增区间为(-1,+∞).
当x=-1时,函数f(x)=xex的极小值为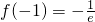 .
.
分析:求出函数的导函数,由导函数等于0求出x的值,以求出的x的值为分界点把原函数的定义域分段,以表格的形式列出导函数在各区间段内的符号及原函数的增减性,从而得到函数的单调区间及极值点,把极值点的坐标代入原函数求极值.
点评:本题考查了利用导数研究函数的单调性与极值,在求出导函数等于0的x值后,借助于表格分析能使解题思路更加清晰,此题是中档题.
f'(x)=(xex)′=x′ex+x(ex)′=ex+xex
令f'(x)=ex+xex=ex(1+x)=0,解得:x=-1.
列表:
| x | (-∞,-1) | -1 | (-1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | 极小值 | ↑ |
当x=-1时,函数f(x)=xex的极小值为
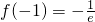 .
.分析:求出函数的导函数,由导函数等于0求出x的值,以求出的x的值为分界点把原函数的定义域分段,以表格的形式列出导函数在各区间段内的符号及原函数的增减性,从而得到函数的单调区间及极值点,把极值点的坐标代入原函数求极值.
点评:本题考查了利用导数研究函数的单调性与极值,在求出导函数等于0的x值后,借助于表格分析能使解题思路更加清晰,此题是中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目