题目内容
若三角形的一个顶点为A(2,3),两条高所在直线的方程为x-2y+3=0和x+y-4=0,求此三角形三边所在直线的方程.
答案:
解析:
解析:
|
解:将点A(2,3)代入两条高所在直线的方程,发现点A不在这两条直线上,因此可设AB边上的高所在直线的方程为x-2y+3=0,AC边上的高所在直线的方程为x+y-4=0. 则AB边所在直线的斜率为-2,方程为y-3=-2(x-2),即2x+y-7=0; AC边所在直线的斜率为1,方程为y-3=x-2,即x-y+1=0. 故BC边所在直线的方程为 故三角形三边所在直线的方程分别为2x+y-7=0,x-y+1=0及x+2y-5=0. |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

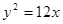 上,则这个三角形的面积为 。
上,则这个三角形的面积为 。 ,两条高所在的直线方程
,两条高所在的直线方程 和
和 ,试求此三角形三边所在的直线方程;
,试求此三角形三边所在的直线方程;