题目内容
在等边三角形ABC中,M、N、P分别为AB、AC、BC的中点,沿MN将△AMN折起,使得面AMN与面MNCB所成的二面角的余弦值为
,则直线AM与NP所成角α应满足______.
| 1 |
| 3 |

设等边三角形ABC的边长为4,取MN的中点O,连接AO,OP,则cos∠AOP=
| 1 |
| 3 |
∵AO=OP=
| 3 |
∴AP=
AO2+PO2-2AO•PO•
|
连接NP,则
∵N、P分别为AAC、BC的中点,∴NP∥MB
∴∠AMB(或其补角)是直线AM与NP所成角α
∵AM=MB=2
∴∠AMB=60°
故答案为:60°

练习册系列答案
相关题目
在等边三角形ABC中,M、N、P分别为AB、AC、BC的中点,沿MN将△AMN折起,使得面AMN与面MNCB所在二面角的余弦值为
,则直线AM与NP所成角的大小为( )
| 1 |
| 3 |
| A、90° | ||||
| B、60° | ||||
C、arccos
| ||||
D、arccos
|
 在等边三角形ABC中,AB=a,O为△ABC的中心,过O的直线交AB于M,交AC于N,求
在等边三角形ABC中,AB=a,O为△ABC的中心,过O的直线交AB于M,交AC于N,求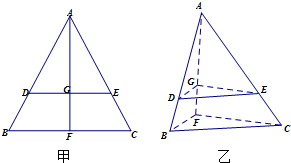 如图甲,在等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC上的点,AF与DE交于点G,将△ABF沿AF折起,得到如图乙所示的三棱锥A-BCF,证明:DE∥平面BCF.
如图甲,在等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC上的点,AF与DE交于点G,将△ABF沿AF折起,得到如图乙所示的三棱锥A-BCF,证明:DE∥平面BCF.