题目内容
15.已知F1,F2是椭圆$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{m}^{2}-4}$=1(m>2)的左,右焦点,点P在椭圆上,若|PF1|•|PF2|=2$\sqrt{3}$m,则该椭圆离心率的取值范围为$[\frac{\sqrt{7}-\sqrt{3}}{2},\frac{\sqrt{3}}{3}]$.分析 由椭圆的定义可得|PF1|+|PF2|=2m,利用基本不等式的性质可得:|PF1|+|PF2|≥$2\sqrt{|P{F}_{1}||P{F}_{2}|}$,化简整理即可得出.另一方面:设∠F1PF2=θ,由余弦定理可得:$|P{F}_{1}{|}^{2}$+$|P{F}_{2}{|}^{2}$-2|PF1||PF2|cosθ=(2c)2=16.
$|P{F}_{1}{|}^{2}$+$|P{F}_{2}{|}^{2}$+2|PF1||PF2|=4m2.相减利用三角函数的单调性、不等式的解法即可得出.
解答 解:由椭圆的定义可得|PF1|+|PF2|=2m,
∴2m=|PF1|+|PF2|≥$2\sqrt{|P{F}_{1}||P{F}_{2}|}$=2$\sqrt{2\sqrt{3}m}$,
化为${m}^{2}≥2\sqrt{3}m$,又m>2,
解得$m≥2\sqrt{3}$.
另一方面:设∠F1PF2=θ,
由余弦定理可得:$|P{F}_{1}{|}^{2}$+$|P{F}_{2}{|}^{2}$-2|PF1||PF2|cosθ=(2c)2=16.
$|P{F}_{1}{|}^{2}$+$|P{F}_{2}{|}^{2}$+2|PF1||PF2|=4m2.
相减可得:1+cosθ=$\frac{{m}^{2}-4}{\sqrt{3}m}$.
∵θ∈[0,π),
∴0<$\frac{{m}^{2}-4}{\sqrt{3}m}$≤2.m≥2$\sqrt{3}$
∴2≤m≤$\sqrt{3}$+$\sqrt{7}$.
∴$e=\frac{c}{a}$=$\sqrt{1-\frac{{m}^{2}-4}{{m}^{2}}}$=$\frac{2}{m}$∈$[\frac{\sqrt{7}-\sqrt{3}}{2},\frac{\sqrt{3}}{3}]$,
∴该椭圆离心率的取值范围为$[\frac{\sqrt{7}-\sqrt{3}}{2},\frac{\sqrt{3}}{3}]$,
故答案为:$[\frac{\sqrt{7}-\sqrt{3}}{2},\frac{\sqrt{3}}{3}]$.
点评 本题考查了椭圆的定义标准方程及其性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案
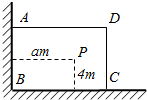 如图,有-直角墙角,两边的长度足够长,在P处有-棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成-个矩形的花围ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花围的面积为y平方米.
如图,有-直角墙角,两边的长度足够长,在P处有-棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成-个矩形的花围ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花围的面积为y平方米.