题目内容
m是正实数.若椭圆
+
=1的焦距为4,则m=
| x2 |
| m+1 |
| y2 |
| 9 |
12或4
12或4
.分析:分椭圆的焦点在x轴或y轴两种情况,根据椭圆基本量的关系建立关于m的方程,解之即可得到实数m的值.
解答:解:①当椭圆焦点在x轴上时,
a2=m+1,b2=9,得c=
=
∴焦距2c=2
=4,解之得m=12
②当椭圆焦点在y轴上时,
a2=9,b2=m+1,得c=
=
∴焦距2c=2
=4,解之得m=4
综上所述,得m=12或4
故答案为:12或4
a2=m+1,b2=9,得c=
| a2-b2 |
| m-8 |
∴焦距2c=2
| m-8 |
②当椭圆焦点在y轴上时,
a2=9,b2=m+1,得c=
| a2-b2 |
| 8-m |
∴焦距2c=2
| 8-m |
综上所述,得m=12或4
故答案为:12或4
点评:本题给出含有字母参数m的方程,在已知焦距的情况下求参数的值,着重考查了椭圆的标准方程和基本概念,属于基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
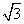 ),它们在x轴上有共同焦点,椭圆的对称轴是坐标轴,
),它们在x轴上有共同焦点,椭圆的对称轴是坐标轴,