题目内容
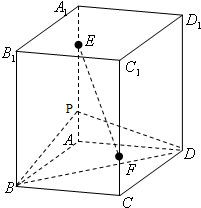 直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.(1)证明:BD⊥EF;
(2)P在棱AA1上,且AP=2,若EF∥平面PBD,求:CF;
(3)多面体AE-BCFB1的体积V是否为常数?若是,求这个常数,若不是,求V的取值范围.
分析:(1)由题意知AC⊥BD,AA1⊥平面ABCD得BD⊥平面AA1C1C,再证BD⊥EF;
(2)由EF∥平面PBD得EF∥PO,再由题意构造中位线得QC∥PO,证出EFCQ为平行四边形再由题意求CF;
(3)把多面体AE-BCFB1分割成四棱锥B1-AEFC和三棱锥B1-ABC,分别求出体积在求和.
(2)由EF∥平面PBD得EF∥PO,再由题意构造中位线得QC∥PO,证出EFCQ为平行四边形再由题意求CF;
(3)把多面体AE-BCFB1分割成四棱锥B1-AEFC和三棱锥B1-ABC,分别求出体积在求和.
解答:证明:(1)连接AC,∵ABCD是菱形,∴AC⊥BD,
∵ABCD-A1B1C1D1是直四棱柱,∴AA1⊥平面ABCD,
∵BD?ABCD,∴AA1⊥BD(2分),
∵AA1∩AC=A,∴BD⊥平面AA1C1C,
∵EF?平面AA1C1C,∴BD⊥EF(4分).
(2)连AC交BD与O,再取AA1中点Q,连QC,
∵EF∥平面PBD,平面PBD∩平面ACEF=PO,
∴EF∥PO;∵AQ=4,AP=2,
∴QC∥PO,∴EF∥QC
又∵AA1∥CC1
∴EFCQ为平行四边形,∴FC=EQ
∵AE+CF=8
∴CF=2(8分)
(3) 多面体AE-BCFB1是四棱锥B1-AEFC和三棱锥B1-ABC的组合体,
由题意,BB1=8,AB=2,BB1三棱锥B1-ABC的高,BO是四棱锥B1-AEFC的高,
∴V=
×S△ABC×BB1+
×SAEFC×BO=
是常数.(12分)
∵ABCD-A1B1C1D1是直四棱柱,∴AA1⊥平面ABCD,
∵BD?ABCD,∴AA1⊥BD(2分),
∵AA1∩AC=A,∴BD⊥平面AA1C1C,
∵EF?平面AA1C1C,∴BD⊥EF(4分).
(2)连AC交BD与O,再取AA1中点Q,连QC,
∵EF∥平面PBD,平面PBD∩平面ACEF=PO,
∴EF∥PO;∵AQ=4,AP=2,
∴QC∥PO,∴EF∥QC
又∵AA1∥CC1
∴EFCQ为平行四边形,∴FC=EQ
∵AE+CF=8
∴CF=2(8分)
(3) 多面体AE-BCFB1是四棱锥B1-AEFC和三棱锥B1-ABC的组合体,
由题意,BB1=8,AB=2,BB1三棱锥B1-ABC的高,BO是四棱锥B1-AEFC的高,
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
16
| ||
| 3 |
点评:本题考查了线线、线面的垂直和平行的定理应用,如何实现线线和线面垂直和平行的转化;求多面体体积时常用分割法求,注意几何体的高.

练习册系列答案
相关题目
 如图,在直四棱柱ABCD-A′B′C′D′中,底面ABCD为梯形,BC∥AD,AA′=AB=
如图,在直四棱柱ABCD-A′B′C′D′中,底面ABCD为梯形,BC∥AD,AA′=AB= 已知直四棱柱ABCD-A′B′C′D′,四边形ABCD为正方形,AA′=2AB=2,E为棱CC′的中点.
已知直四棱柱ABCD-A′B′C′D′,四边形ABCD为正方形,AA′=2AB=2,E为棱CC′的中点. 已知直四棱柱ABCD-A′B′C′D′的底面是菱形,∠ABC=60°,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
已知直四棱柱ABCD-A′B′C′D′的底面是菱形,∠ABC=60°,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.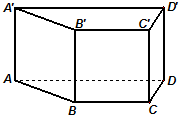 在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2.
在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2. 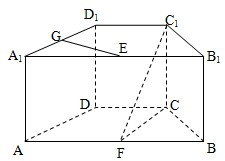 (2009•崇明县一模)如图,在直四棱柱ABCD-A'B'C'D'中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.
(2009•崇明县一模)如图,在直四棱柱ABCD-A'B'C'D'中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.