Question

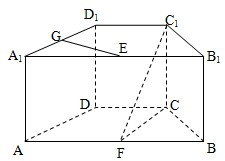（2009•崇明县一模）如图，在直四棱柱ABCD-A'B'C'D'中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA₁=2，E、F、G分别是棱A₁B₁、AB、A₁D₁的中点．
（1）证明：直线GE⊥平面FCC₁；
（2）求二面角B-FC₁-C的大小．

Answer 1

分析：（1）构建空间直角坐标系，用坐标表示向量，再证明：

GE

•

CC1

=0，

GE

•

CF

=0
（2）先求两平面的法向量，再利用数量积公式可求二面角B-FC₁-C的大小

解答：解：（1）以D为坐标原点，建立空间直角坐标系．
则G(

3

2

，-

1

2

，2)，E(

3

，1，2)，

GE

=(

3

2

，

3

2

，0)；C(0，2，0)，C1(0，2，2)，F(

3

，1，0)；

CC1

=(0，0，2)，

CF

=(

3

，-1，0)
所以

GE

•

CC1

=0，

GE

•

CF

=0
所以GE垂直平面FCC₁．
（2）平面FCC₁的法向量n1=(

3

2

，

3

2

，0)；
设平面BFC₁的法向量为

n2

=(x，y，z)

BF

=(0，

3

，0)，

C1F

=(

3

，-1，-2)
由

n2

•

BF

=0，

n2

•

C1F

=0得一个法向量

n2

=(2，0，

3

)cosθ=|

n1•n2

|n1|•|n2|

|=

7

7

；θ=arccos

7

7

．
所以二面角B-FC₁-C的大小为arccos

7

7

．

点评：本题以直四棱柱为载体，考查线面垂直，考查面面角，关键是构建空间直角坐标系，利用公式求解．