题目内容
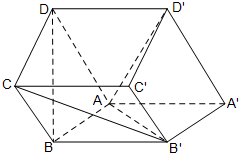 如图,在直四棱柱ABCD-A′B′C′D′中,底面ABCD为梯形,BC∥AD,AA′=AB=
如图,在直四棱柱ABCD-A′B′C′D′中,底面ABCD为梯形,BC∥AD,AA′=AB=| 2 |
(Ⅰ)求证:DB⊥面ABB'A';
(Ⅱ)求证:AD'⊥B'C;
(Ⅲ)求二面角D-AB'-B的正切值.
分析:(I)根据面与面垂直,得到直线AB为直线AD在面ABB'A'上的射影,得到∠DAB=45°,根据线与线垂直,做出线与面垂直.
(II)做出辅助线,取AD中点E,连接CE、A'E,得到线与线垂直,根据直四棱柱ABCD-A'B'C'D'侧面AA'D'D为矩形,得到线与线垂直.
(III)首先做出二面角的平面角,过点B作BF⊥AB'交AB'于F,连接DF,得到AB'⊥面DBF,得到∠BFD为所求二面角的平面角,在可解的三角形中做出角的正切值.
(II)做出辅助线,取AD中点E,连接CE、A'E,得到线与线垂直,根据直四棱柱ABCD-A'B'C'D'侧面AA'D'D为矩形,得到线与线垂直.
(III)首先做出二面角的平面角,过点B作BF⊥AB'交AB'于F,连接DF,得到AB'⊥面DBF,得到∠BFD为所求二面角的平面角,在可解的三角形中做出角的正切值.
解答:
 解:(Ⅰ)证明:∵面ABD⊥面ABB'A',∴直线AB为直线AD在面ABB'A'上的射影,
解:(Ⅰ)证明:∵面ABD⊥面ABB'A',∴直线AB为直线AD在面ABB'A'上的射影,
∴∠DAB=45°,由AB=
,AD=2知,
DB⊥AB,∴DB⊥面AB'A'
(Ⅱ)证明:取AD中点E,连接CE、A'E,
∵BC∥AD,AD=2BC,
∴BC∥AE且BC=AE,
∴EC∥AB∥A'B'且EC=A'B',∴A'E∥B'C,
又直四棱柱ABCD-A'B'C'D'侧面AA'D'D为矩形,
tan∠AA′E=
=
,tan∠AD′A′=
∠AA'E=∠AD'A',∠AA'E+∠D'AA'=∠AD'A'+∠D'AA'=90°
∴AD'⊥A'E,∴AD'⊥B'C
(Ⅲ)∵DB⊥面ABB'A'且BD=
过点B作BF⊥AB'交AB'于F,连接DF,
则AB'⊥面DBF,
∴AB'⊥DF,∠BFD为所求二面角的平面角,
又BF=
=
=1
∴tan∠BFD=
=
,即二面角D-AB'-B的正切值为
.

 解:(Ⅰ)证明:∵面ABD⊥面ABB'A',∴直线AB为直线AD在面ABB'A'上的射影,
解:(Ⅰ)证明:∵面ABD⊥面ABB'A',∴直线AB为直线AD在面ABB'A'上的射影,∴∠DAB=45°,由AB=
| 2 |
DB⊥AB,∴DB⊥面AB'A'
(Ⅱ)证明:取AD中点E,连接CE、A'E,
∵BC∥AD,AD=2BC,
∴BC∥AE且BC=AE,
∴EC∥AB∥A'B'且EC=A'B',∴A'E∥B'C,
又直四棱柱ABCD-A'B'C'D'侧面AA'D'D为矩形,
tan∠AA′E=
| 1 | ||
|
| ||
| 2 |
| ||
| 2 |
∠AA'E=∠AD'A',∠AA'E+∠D'AA'=∠AD'A'+∠D'AA'=90°
∴AD'⊥A'E,∴AD'⊥B'C
(Ⅲ)∵DB⊥面ABB'A'且BD=
| 2 |
过点B作BF⊥AB'交AB'于F,连接DF,
则AB'⊥面DBF,
∴AB'⊥DF,∠BFD为所求二面角的平面角,
又BF=
| AB•BB′ |
| AB′ |
| ||||
| 2 |
∴tan∠BFD=
| BD |
| BF |
| 2 |
| 2 |
点评:本题考查二面角的求法和线与面之间的关系,本题解题的关键是理解求二面角的三个环节,首先做出二面角的平面角,把平面角放到一个可解的三角形中,解出平面角.

练习册系列答案
相关题目
 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明:
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明: 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点. 15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点.
15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点. (2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.
(2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.