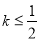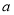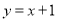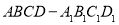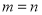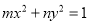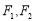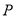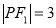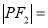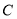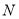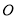题目内容
已知正方体
，点
，
，
分别是线段
，
和
上的动点，观察直线
与
，与
．给出下列结论：
①对于任意给定的点，存在点
，使得
；
②对于任意给定的点
，存在点，使得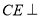
；
③对于任意给定的点
，存在点
，使得
；
④对于任意给定的点
，存在点，使得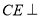
．
其中正确结论的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】
试题分析：因为对任意的E点，则直线CE所形成的轨迹都在平面
上，所以要使得
，即要存在平面，显然是不成立的，所以①不正确；因为对于任意点
，由
形成的轨迹在平面
上，所以要存在
只需要
即可，这显然可以成立，所以②正确.同理③只要G点移到
点即可成立，所以③正确.与①类似④不成立.故选B.
考点：1.线面垂直的判定.2.线线垂直的判定.3.线动成面的思维.
练习册系列答案
科学实验活动册系列答案
相关题目
