题目内容
(I)设a>0,b>0求证:a3+b3≥a2b+ab2
(II)设a>0,b>0,c>0,且a,b,c不且相等,求证: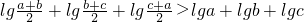 .
.
证明:(Ⅰ)∵a3+b3-a2b-ab2=a2(a-b)-b2(a-b)=(a-b)2(a+b),
又a>0,b>0,
∴a+b>0,(a-b)2≥0,
∴(a-b)2(a+b)≥0,
∴a3+b3≥a2b+ab2;
(Ⅱ)∵a>0,b>0,c>0,
∴ ≥
≥ ,
,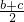 ≥
≥ ,
, ≥
≥ ,
,
∴lg ≥lg
≥lg =
= (lga+lgb)①,同理可得lg
(lga+lgb)①,同理可得lg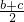 ≥
≥ (lab+lgc)②,lg
(lab+lgc)②,lg ≥
≥ (lga+lgc)③,
(lga+lgc)③,
①+②+③得:
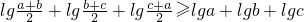
又a,b,c不全相等,
∴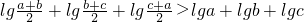 .
.
分析:(Ⅰ)a3+b3≥a2b+ab2?a3+b3-a2b-ab2≥0?(a-b)2(a+b)≥0,结合a>0,b>0,问题即可解决;
(Ⅱ)a>0,b>0,c>0,? ≥
≥ ,
,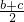 ≥
≥ ,
, ≥
≥ ,于是lg
,于是lg ≥lg
≥lg =
= (lga+lgb),同理可得lg
(lga+lgb),同理可得lg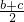 ≥
≥ (lab+lgc),lg
(lab+lgc),lg ≥
≥ (lga+lgc),又a,b,c不且相等,同向不等式相加即可.
(lga+lgc),又a,b,c不且相等,同向不等式相加即可.
点评:本题考查不等式的证明,着重考查证明不等式的方法:作差法与综合法,注重基本不等式性质的应用,属于中档题.
又a>0,b>0,
∴a+b>0,(a-b)2≥0,
∴(a-b)2(a+b)≥0,
∴a3+b3≥a2b+ab2;
(Ⅱ)∵a>0,b>0,c>0,
∴
 ≥
≥ ,
,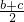 ≥
≥ ,
, ≥
≥ ,
,∴lg
 ≥lg
≥lg =
= (lga+lgb)①,同理可得lg
(lga+lgb)①,同理可得lg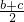 ≥
≥ (lab+lgc)②,lg
(lab+lgc)②,lg ≥
≥ (lga+lgc)③,
(lga+lgc)③,①+②+③得:
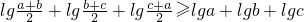
又a,b,c不全相等,
∴
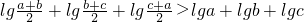 .
.分析:(Ⅰ)a3+b3≥a2b+ab2?a3+b3-a2b-ab2≥0?(a-b)2(a+b)≥0,结合a>0,b>0,问题即可解决;
(Ⅱ)a>0,b>0,c>0,?
 ≥
≥ ,
,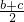 ≥
≥ ,
, ≥
≥ ,于是lg
,于是lg ≥lg
≥lg =
= (lga+lgb),同理可得lg
(lga+lgb),同理可得lg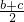 ≥
≥ (lab+lgc),lg
(lab+lgc),lg ≥
≥ (lga+lgc),又a,b,c不且相等,同向不等式相加即可.
(lga+lgc),又a,b,c不且相等,同向不等式相加即可.点评:本题考查不等式的证明,着重考查证明不等式的方法:作差法与综合法,注重基本不等式性质的应用,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
