题目内容
某商店经销一种洗衣粉,年销售总量为500包,每包进价为2元、销售价为3元,全年分若干次进货,每次进货均为x包,已知每次进货运输费为5元,全年保管费为x元.设利润为y元,则y关于x的表达式是
y=500-(
+x)
| 2500 |
| x |
y=500-(
+x)
,利润y的最大值是| 2500 |
| x |
400
400
元.分析:由题意,利润y等于销售利润减去运输费与保管费,利用基本不等式可求利润y的最大值.
解答:解:由于每次进货均为x包,已知每次进货运输费为5元,则运输费为
× 5=
元,从而利润为y=500-(
+x),利用基本不等式有y≤500-100=400,当且仅当x=50时,利润y取最大值,
故答案为:y=500-(
+x),400.
| 500 |
| x |
| 2500 |
| x |
| 2500 |
| x |
故答案为:y=500-(
| 2500 |
| x |
点评:本题主要考查函数模型的建立,考查利用基本不等式求函数的最大值,属于基础题.

练习册系列答案
相关题目
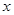 包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5
包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5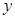 (元)表示为每次进货量
(元)表示为每次进货量