题目内容
某商店经销一种洗衣粉,年销售总量为6000包,每包进价为2.8元、销售价为3.4元,全年分若干次进货、每次进货均为x包,已知每次进货运输费为62.5元,全年保管费为1.5x元,为使利润最大,则x=
500
500
.分析:由于利润=毛利-总运输费-全年保管费故求出毛利,总运输费,全年保管费即可得出利润关于x的表达式然后再根据表达式的形式选择恰当的方法求其取得最大值时对应的x的值即可.
解答:解:设获得的利润为y元,根据题意可得毛利=(3.4-2.8)×6000,总运输费=
×62.5,全年保管费为1.5x
∴y=(3.4-2.8)×6000-
×62.5-1.5x=-1.5(x+
)+3600,
∵x>0
∴x+
≥2
=1000(元)(当且仅当x=
即x=500时取等号)
∴-1.5(x+
)+3600≤2500即y≤2500
即当x=500时函数取得最大值2500
| 6000 |
| x |
∴y=(3.4-2.8)×6000-
| 6000 |
| x |
| 400×625 |
| x |
∵x>0
∴x+
| 400×625 |
| x |
x•
|
| 400×625 |
| x |
∴-1.5(x+
| 400×625 |
| x |
即当x=500时函数取得最大值2500
点评:本题主要考察了基本不等式在求最值中的应用,属常考题型,较难.解题的关键是首先根据题中条件建立符合题意的函数模型y=-1.5(x+
)+3600然后再利用基本不等式求解同时要注意利用基本不等式求解时的三步曲“一正,二定,三相等”!
| 400×625 |
| x |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
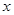 包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5
包,已知每次进货的运输劳务费为62.5元,全部洗衣粉一年的保管费为1.5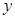 (元)表示为每次进货量
(元)表示为每次进货量