题目内容
已知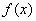 为
为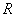 上的偶函数,当
上的偶函数,当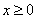 时,
时,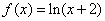 .
.
(1)当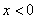 时,求
时,求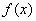 的解析式;
的解析式;
(2)当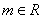 时,试比较
时,试比较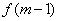 与
与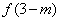 的大小;
的大小;
(3)求最小的整数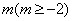 ,使得存在实数
,使得存在实数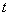 ,对任意的
,对任意的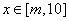 ,都有
,都有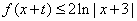 .
.
1)当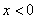 时,
时, ,
, .
.
又 ,所以
,所以 .
.
(2)当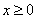 时,
时,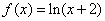 单调递增,而
单调递增,而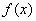 是偶函数,所以
是偶函数,所以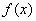 在
在 上单调递减,所以
上单调递减,所以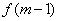 >
>
 .
.
所以当 时,
时,  ;
;
当 时,
时,  ;
;
当 时,
时,  ;
;
当 时,
时,  .
.
(3) 当 时,
时, ,则由
,则由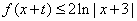 ,
,
得 ,即
,即 对
对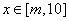 恒成立.
恒成立.
从而有 对
对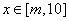 恒成立,因为
恒成立,因为 ,
,
所以 .
.
因为存在这样的t ,所以 ,即
,即 .
.
又 ,所以适合题意的最小整数
,所以适合题意的最小整数 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
观察分析下表中的数据:猜想一般凸多面体中F,V,E所满足的等 式是________.
式是________.
| 多面体 | 面数(F) | 顶点数(V) | 棱数(E) |
| 三棱柱 | 5 | 6 | 9 |
| 五棱锥 | 6 | 6 | 10 |
| 立方体 | 6 | 8 | 12 |
 派方法共有________种.
派方法共有________种.
 上是单调增函数,若
上是单调增函数,若 ,求
,求 的取值范围.
的取值范围. 当
当 时,
时, ,则实数
,则实数 ②
②

 .其中为假命题的个数共有________个.
.其中为假命题的个数共有________个. 与复数
与复数 对应,动点
对应,动点 与复数
与复数 对应,那么满足不等式
对应,那么满足不等式 的点
的点 中,圆C的方程为
中,圆C的方程为 .若直线
.若直线 上存在点
上存在点 ,使过
,使过 的取值范围是 .
的取值范围是 .