题目内容
(本小题满分12分)设函数
 其中
其中
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ) 讨论 的极值.
的极值.
解:由已知得 [来源:Z&xx&k.Com] ,令
,令 ,解得
,解得  .……………………………2分
.……………………………2分
(1)当 时,
时, ,
, 在
在 上单调递增.
上单调递增.
当 时,
时, ,
, 随
随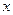 的变化情况如下表:[来源:Z|xx|k.Com]
的变化情况如下表:[来源:Z|xx|k.Com]
从上表可知,函数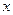

0 



+ 0 
0 


极大值 
极小值 
 在
在 上单调递增;在
上单调递增;在 上单调递减;在
上单调递减;在 上单调递增.…………………………………7分
上单调递增.…………………………………7分
(2)由(1)知,
当 时,函数
时,函数 没有极值.
没有极值.
当 时,函数
时,函数 在
在 处取得极大值,在
处取得极大值,在 处取得极小值
处取得极小值 .……12分
.……12分
解析

练习册系列答案
相关题目
 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M 处的切线方程为
处的切线方程为 .
. 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数 为奇函数,且
为奇函数,且 在
在 处取得极大值2.
处取得极大值2. 的解析式;
的解析式; ,求函数
,求函数 的单调区间。
的单调区间。 与曲线
与曲线 交于点
交于点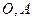 .直线
.直线 与曲线
与曲线 分别相交于点
分别相交于点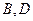 .
. 的面
的面 积
积 与
与 的函数关系
的函数关系 ;
; 的单调性,并求
的单调性,并求
 分15分)已知函数
分15分)已知函数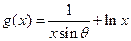 在
在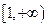 上为增函数,且
上为增函数,且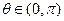 ,
,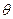 为常数,
为常数,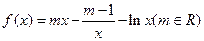 .
.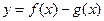 在
在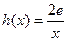 ,若在
,若在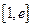 上至少存在一个
上至少存在一个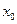 ,使得
,使得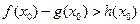 成立,求的m取值范围.
成立,求的m取值范围. ,曲线在点M处的切线恰好与直线
,曲线在点M处的切线恰好与直线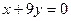 垂直
垂直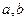 的值
的值 )若函数
)若函数 的取值范围。
的取值范围。 。
。 m恒成立,求m的最大值;
m恒成立,求m的最大值; 。
。 处的切线垂直y轴,求a的值;
处的切线垂直y轴,求a的值; ;
; ,
, ,求实数b的取值范围。
,求实数b的取值范围。
 的最小值;(2)若
的最小值;(2)若 在
在 内恒成立,求
内恒成立,求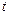 的取值范围
的取值范围