题目内容
（本小题满分12分）
（1）求
的最小值；(2)若≥
在
内恒成立，求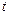
的取值范围
解：（1）函数的定义域为
设
当
变化时，
值的变化情况如下表：
所以，当
时，
（2）由≥对恒成立
≤
令
得
为
上的减函数.
∴当时，
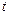有最小值2，得≤2，≤1，
故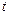的取值范围是
解析
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
轻巧夺冠周测月考直通中考系列答案题目内容
（本小题满分12分）
（1）求的最小值；(2)若≥在内恒成立，求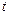的取值范围
解：（1）函数的定义域为
设 当变化时，值的变化情况如下表：
所以，当时，
（2）由≥对恒成立≤令 得为上的减函数.
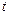∴当时，有最小值2，得≤2，≤1，
故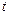的取值范围是
解析
轻巧夺冠周测月考直通中考系列答案
其中
的单调区间；
(
)（
为自然对数的底数）
的极值
,
(
)
的方程
是否有解，并说明理由
，其中
，若
在区间
上不是单调函数，求
的取值范围.
是否存在
，存在唯一的非零
使得
成立，若存在，求
资、车损等其他费用平均每小时300元．已知燃油价格为每升(L)7.5元．
的费用为y(元)(不计返程费用)，将y表示成速度v的函数
关系式；
的单调区间；
恒成立，试确定实数
的取值范围；
时，车流速度
是车流密度
的一次函数．
时，求函数
的表达式；
（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）
可以达到最大，并求出最
大值．（精确到1辆/小时）
，
的奇偶性；
的方
程
有实数解，求实数
的取值范围．
，其中
，
，已知对所有的有序正整数对
满足下述条件:①
，②若
，
；③
，则
.