题目内容
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且2cosAcosC(tanAtanC﹣1)=1.
(Ⅰ)求B的大小;
(Ⅱ)若 ![]() ,
, ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】解:(Ⅰ)由2cosAcosC(tanAtanC﹣1)=1得:2cosAcosC( ![]() ﹣1)=1, ∴2(sinAsinC﹣cosAcosC)=1,即cos(A+C)=﹣
﹣1)=1, ∴2(sinAsinC﹣cosAcosC)=1,即cos(A+C)=﹣ ![]() ,
,
∴cosB=﹣cos(A+C)= ![]() ,
,
又0<B<π,
∴B= ![]() ;
;
(Ⅱ)由余弦定理得:cosB= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
又a+c= ![]() ,b=
,b= ![]() ,
,
∴ ![]() ﹣2ac﹣3=ac,即ac=
﹣2ac﹣3=ac,即ac= ![]() ,
,
∴S△ABC= ![]() acsinB=
acsinB= ![]() ×
× ![]() ×
× ![]() =
= ![]()
【解析】(Ⅰ)已知等式括号中利用同角三角函数间基本关系切化弦,去括号后利用两角和与差的余弦函数公式化简,再由诱导公式变形求出cosB的值,即可确定出B的大小;(Ⅱ)由cosB,b的值,利用余弦定理列出关系式,再利用完全平方公式变形,将a+b以及b的值代入求出ac的值,再由cosB的值,利用三角形面积公式即可求出三角形ABC面积.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.

【题目】某车间为了给贫困山区的孩子们赶制一批爱心电子产品,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 |
| 3 | 4 |
|
经统计发现零件个数![]() 与加工时间
与加工时间![]() 具有线性相关关系.
具有线性相关关系.
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)试预测加工10个零件需要多少时间.
利用公式: ,
,![]()
【题目】全世界越来越关注环境保护问题,某监测站点于2018年1月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:
空气质量指数( |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
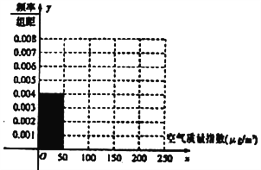
(1)根据所给统计表和频率分布直方图中的信息求出![]() ,
,![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的众数和中位数;
(3)在空气质量指数分别属于![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,再从中任意选取
天,再从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.