题目内容
在 中,满足
中,满足 ,
, 是
是 边上的一点.
边上的一点.
(Ⅰ)若 ,求向量
,求向量 与向量
与向量 夹角的正弦值;
夹角的正弦值;
(Ⅱ)若 ,
, =m
(m为正常数) 且
=m
(m为正常数) 且 是
是 边上的三等分点.,求
边上的三等分点.,求 值;
值;
(Ⅲ)若 且
且 求
求 的最小值。
的最小值。
【答案】
(Ⅰ)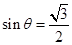 ;
;
(Ⅱ)(1)当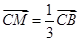 时,则
时,则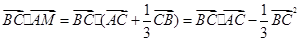 =
=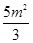 ;
;
(2)当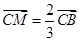 时,则
时,则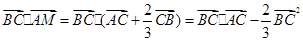 =
=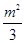 ;
;
(Ⅲ)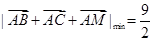 .
.
【解析】
(Ⅰ)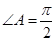 ,
,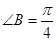 可得
可得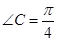 ,
,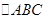 是等腰直角三角形,令
是等腰直角三角形,令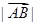 =
=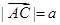 ;
;
(Ⅱ)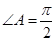 ,
,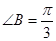 ,
,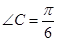 ,
,
利用30°的直角三角形的性质令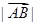 =m所以
=m所以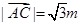 ,
,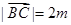 ,
,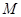 是
是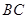 边上的三等分点.分类讨论:
边上的三等分点.分类讨论: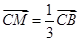 或
或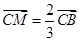 ;
;
(Ⅲ)注意到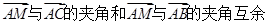 ,是解题的关键,
,是解题的关键,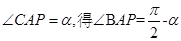 ,求
,求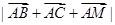 通常用平方的方法。
通常用平方的方法。
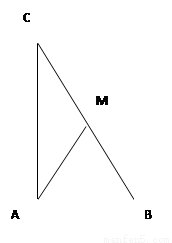
(Ⅰ)解:设向量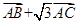 与向量
与向量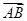 的夹角为
的夹角为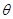 ,则
,则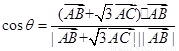
令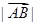 =
=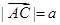 ,得
,得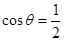 ,又
,又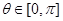 ,则
,则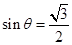 为所求……………2分
为所求……………2分
(Ⅱ)解:因为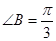 ,
,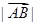 =m所以
=m所以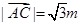 ,
,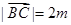
(1)当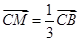 时,则
时,则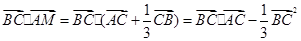 =
=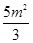 ;--2分
;--2分
(2)当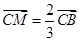 时,则
时,则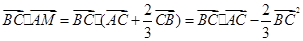 =
=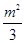 ;---2分
;---2分
(Ⅲ)解:设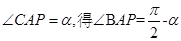 ,因为
,因为
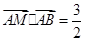 ,
,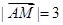 ;
;
所以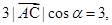 即
即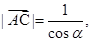 于是
于是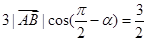 得
得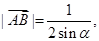
从而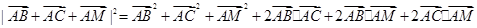 ---2分
---2分
=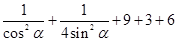 =
=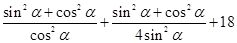
=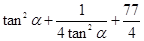 …………………………………2分
…………………………………2分
令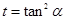 ,
,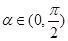 则
则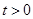 ,则函数
,则函数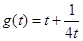 ,在
,在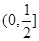 递减,在
递减,在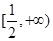 上递增,所以
上递增,所以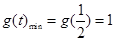 从而当
从而当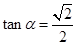 时,
时,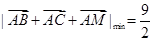 ………………2分
………………2分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,满足:
中,满足: ,
, 是
是 的中点.
的中点. ,求向量
,求向量 与向量
与向量 的夹角的余弦值;
的夹角的余弦值; 是
是 ,且
,且 ,求
,求 的最小值.
的最小值. 中,满足
中,满足 ,
, 是
是 边上的一点.
边上的一点. ,求向量
,求向量 与向量
与向量 夹角的正弦值;
夹角的正弦值; ,
, =m (m为正常数) 且
=m (m为正常数) 且 值;
值; 且
且 求
求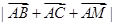 的最小值。
的最小值。 ,则
,则
 ,得
,得 ,又
,又 ,则
,则 为所求
为所求 ,
,
 时,则
时,则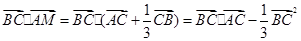 =
=
 时,则
时,则 =
=
 ,因为
,因为
 ,
, 即
即 于是
于是 得
得

 =
= =
=
 …………………………………2分
…………………………………2分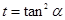 ,
, 则
则 ,则函数
,则函数 ,在
,在 递减,在
递减,在 上递增,所以
上递增,所以 从而当
从而当 时,
时,
 中,满足
中,满足 ,
, 是
是 中点.
中点. ,求向量
,求向量 与向量
与向量 的夹角的余弦值;
的夹角的余弦值; 是线段
是线段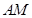 上任意一点,且
上任意一点,且 ,求
,求 的最小值;
的最小值; 是
是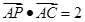 ,
,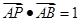 ,
, ,求
,求 的最小值.
的最小值.