题目内容
(14分)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率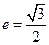 .直线
.直线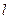 :
: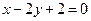 与椭圆C相交于
与椭圆C相交于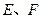 两点, 且
两点, 且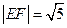
(1)求椭圆C的方程
(2)点P(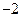 ,0),A、B为椭圆C上的动点,当
,0),A、B为椭圆C上的动点,当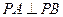 时,求证:直线AB恒过一个定点.并求出该定点的坐标.
时,求证:直线AB恒过一个定点.并求出该定点的坐标.
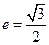 .直线
.直线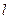 :
: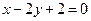 与椭圆C相交于
与椭圆C相交于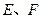 两点, 且
两点, 且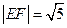
(1)求椭圆C的方程
(2)点P(
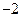 ,0),A、B为椭圆C上的动点,当
,0),A、B为椭圆C上的动点,当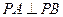 时,求证:直线AB恒过一个定点.并求出该定点的坐标.
时,求证:直线AB恒过一个定点.并求出该定点的坐标. ,
,
解:(1)设椭圆方程为 (a>b>0),
(a>b>0),

 令
令 则
则
 …………2分
…………2分
由 得:
得: ……………………………… 4分
……………………………… 4分

 网
网


椭圆C的方程是: …………………………………… 7分
…………………………………… 7分
(2) 当直线l不垂直于x轴时,设 :
:


 得
得


 …………………… 10分
…………………… 10分

 网
网

当 时,
时, 恒过定点
恒过定点
当 时,
时, 恒过定点
恒过定点 ,不符合题意舍去 … 12分
,不符合题意舍去 … 12分
当直线l垂直于x轴时,若直线AB: 则AB与椭圆C相交于
则AB与椭圆C相交于 ,
,

 ,满足题意
,满足题意
综上可知,直线 恒过定点,且定点坐标为
恒过定点,且定点坐标为 ……………… 14分
……………… 14分
 (a>b>0),
(a>b>0),

 令
令 则
则
 …………2分
…………2分由
 得:
得: ……………………………… 4分
……………………………… 4分
 网
网

椭圆C的方程是:
 …………………………………… 7分
…………………………………… 7分(2) 当直线l不垂直于x轴时,设
 :
:


 得
得


 …………………… 10分
…………………… 10分
 网
网
当
 时,
时, 恒过定点
恒过定点
当
 时,
时, 恒过定点
恒过定点 ,不符合题意舍去 … 12分
,不符合题意舍去 … 12分当直线l垂直于x轴时,若直线AB:
 则AB与椭圆C相交于
则AB与椭圆C相交于 ,
,

 ,满足题意
,满足题意综上可知,直线
 恒过定点,且定点坐标为
恒过定点,且定点坐标为 ……………… 14分
……………… 14分
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
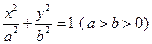 的两个焦点为
的两个焦点为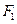 、
、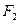 ,短轴两个端点为
,短轴两个端点为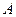 、
、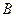 .已知
.已知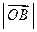 、
、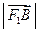 、
、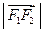 成等比数列,
成等比数列,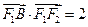 ,与
,与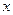 轴不垂直的直线
轴不垂直的直线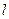 与C 交于不同的两点
与C 交于不同的两点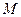 、
、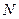 ,记直线
,记直线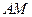 、
、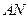 的斜率分别为
的斜率分别为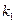 、
、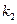 ,且
,且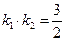 .
.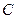 的方程;
的方程;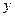 轴相交于定点,并求出定点坐标;
轴相交于定点,并求出定点坐标;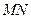 的中点
的中点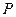 落在四边形
落在四边形 内(包括边界)时,求直线
内(包括边界)时,求直线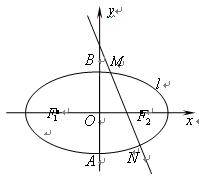
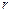 米.市场上,圆柱侧面用料单价为每平方米
米.市场上,圆柱侧面用料单价为每平方米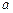 元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为
元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为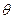 (弧度),总费用为
(弧度),总费用为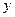 (元).
(元).
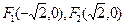 ,平面上动点
,平面上动点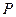 满足
满足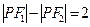 .
.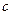 的方程;
的方程;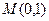 的直线
的直线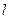 与
与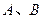 两点,且
两点,且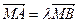 ,当
,当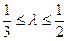 时,求直线
时,求直线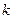 的取值范围.
的取值范围.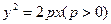 交于
交于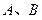 两点,且
两点,且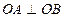 (
(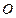 为坐标原点),
为坐标原点),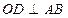 于点
于点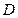 ,点
,点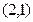
 的方程
的方程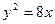 的焦点与双曲线
的焦点与双曲线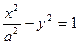 的一个焦点重合,则该双曲线的离心率为 ( )
的一个焦点重合,则该双曲线的离心率为 ( )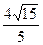
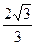

 与圆
与圆 有公共点,则实数a的取值范围是_________.
有公共点,则实数a的取值范围是_________.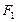 ,
,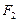 分别是双曲线
分别是双曲线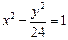 的左、右焦点,
的左、右焦点,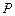 是双曲线上的一点,若
是双曲线上的一点,若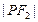 ,
,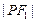 ,
,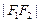 构成公差为正数的等差数列,则
构成公差为正数的等差数列,则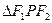 的面积为
的面积为
 的两个顶点为
的两个顶点为 ,
, ,
,


