题目内容
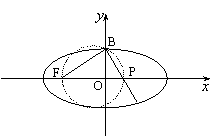
如图,椭圆的中心在坐标原点,长轴端点为A,B,右焦点为F,且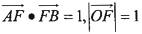 .
.
(I) 求椭圆的标准方程;
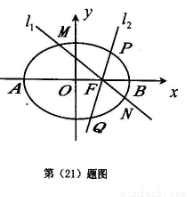
(II)过椭圆的右焦点F作直线 ,直线l1与椭圆分别交于点M,N,直线l2与椭圆分别交于点P,Q,且
,直线l1与椭圆分别交于点M,N,直线l2与椭圆分别交于点P,Q,且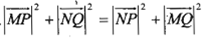 ,求四边形MPNQ的面积S的最小值.
,求四边形MPNQ的面积S的最小值.
【答案】
(Ⅰ)设椭圆的方程为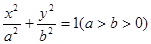 ,则由题意知
,则由题意知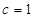 ,
,
又∵ 即
即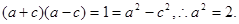 ∴
∴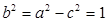 ,
,
故椭圆的方程为: ……………………………………………….2分
……………………………………………….2分
(Ⅱ)设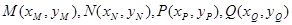 .
.
则由题意, 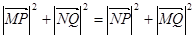 ,
,
即 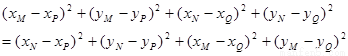
整理得, 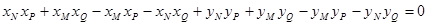
即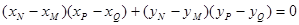
所以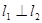 ………………………………………………………………6分
………………………………………………………………6分
(注: 证明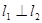 ,用几何法同样得分)
,用几何法同样得分)
①若直线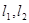 中有一条斜率不存在,不妨设
中有一条斜率不存在,不妨设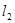 的斜率不存在,则可得
的斜率不存在,则可得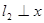 轴,
轴,
∴ 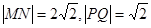 ,
,
故四边形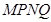 的面积
的面积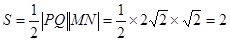 …….…….…….7分
…….…….…….7分
②若直线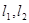 的斜率存在,设直线
的斜率存在,设直线 的方程:
的方程: 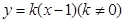 ,则
,则
由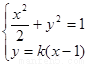 得,
得, 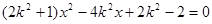
设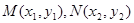 ,则
,则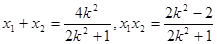
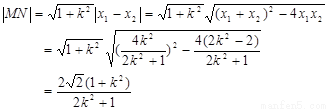 …………….9分
…………….9分
同理可求得,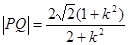 ………………………….10分
………………………….10分
故四边形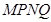 的面积:
的面积:
 取“=”,
取“=”,
综上,四边形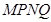 的面积
的面积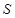 的最小值为
的最小值为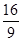
【解析】略

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
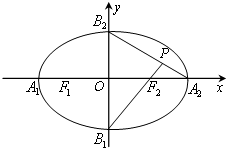 (2013•乌鲁木齐一模)如图,椭圆的中心在坐标原点O,顶点分别是A1,A2,B1,B2,焦点为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为( )
(2013•乌鲁木齐一模)如图,椭圆的中心在坐标原点O,顶点分别是A1,A2,B1,B2,焦点为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为( )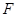 为椭圆的左焦点,
为椭圆的左焦点, 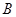 为椭圆的一个顶点,过点
为椭圆的一个顶点,过点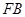 垂直的直线
垂直的直线 交
交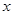 轴于
轴于 点, 且椭圆的长半轴长
点, 且椭圆的长半轴长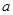 和短半轴长
和短半轴长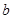 是关于
是关于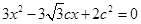 (其中
(其中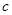 为半焦距)的两个根.
为半焦距)的两个根.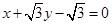 相切,试求椭圆的方程.
相切,试求椭圆的方程.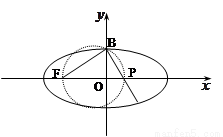
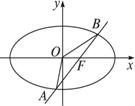
 (1)求椭圆的离心率;
(1)求椭圆的离心率;