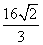题目内容
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为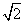 ,且过点(4,-
,且过点(4,-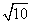 ).
).
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证: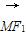 ·
·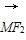 =0;
=0;
(3)求△F1MF2的面积.
[分析] 由离心率为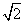 可看出它是等轴双曲线;从此隐含条件入手,可使运算变得简单.
可看出它是等轴双曲线;从此隐含条件入手,可使运算变得简单.
[解析] (1)∵e=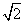 ,∴可设双曲线方程为x2-y2=λ(λ≠0).
,∴可设双曲线方程为x2-y2=λ(λ≠0).
∵过(4,-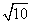 )点,∴16-10=λ,即λ=6,
)点,∴16-10=λ,即λ=6,
∴双曲线方程为x2-y2=6.
(2)证法1:由(1)可知,双曲线中a=b=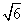 ,
,
∴c=2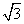 ,∴F1(-2
,∴F1(-2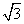 ,0),F2(2
,0),F2(2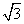 ,0),
,0),
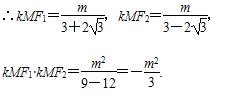 ∵点(3,m)在双曲线上,∴9-m2=6,m2=3.
∵点(3,m)在双曲线上,∴9-m2=6,m2=3.
故kMF1·kMF2=-1,∴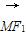 ⊥
⊥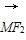 .∴
.∴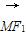 ·
·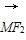 =0.
=0.
证法2:∵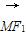 =(-3-2
=(-3-2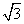 ,-m),
,-m),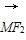 =(2
=(2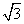 -3,-m),
-3,-m),
∴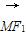 ·
·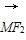 =(3+2
=(3+2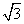 )×(3-2
)×(3-2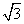 )+m2=-3+m2,
)+m2=-3+m2,
∵M点在双曲线上,∴9-m2=6,即m2-3=0,
∴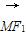 ·
·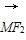 =0.
=0.
(3)△F1MF2的底|F1F2|=4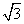 ,
,
△F1MF2的高h=|m|=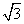 ,∴S△F1MF2=6.
,∴S△F1MF2=6.
[点评] 双曲线的标准方程和几何性质中涉及很多基本量,如“a,b,c,e”等,树立基本量思想对于确定双曲线方程和认识其几何性质有很大帮助.

练习册系列答案
相关题目
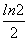 D.ln2
D.ln2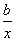 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.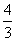 B.2
B.2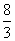 D.
D.