题目内容
18.若实数x,y满足$\left\{\begin{array}{l}{{x}^{2}-xy+{y}^{2}=9}\\{{x}^{2}-{y}^{2}-3x-3y=0}\end{array}\right.$,则实数x的所有取值构成的集合为{-$\sqrt{3}$,0,$\sqrt{3}$,3}.分析 若x2-y2-3x-3y=(x+y)(x-y-3)=0,则x+y=0,或x-y-3=0,分别代入方程x2-xy+y2=9,消去y,可得满足条件的x值.
解答 解:∵x2-y2-3x-3y=(x+y)(x-y-3)=0,
∴x+y=0,或x-y-3=0,
当x+y=0时,y=-x,
则x2-xy+y2=3x2=9,解得:x=±$\sqrt{3}$,
当x-y-3=0时,y=x-3,
则x2-xy+y2=x2-3x+9=9,解得:x=0,或x=3,
综上所述,实数x的所有取值构成的集合为{-$\sqrt{3}$,0,$\sqrt{3}$,3},
故答案为:{-$\sqrt{3}$,0,$\sqrt{3}$,3}
点评 本题考查的知识点二元二次方程的解法,列举法表示集合,难度中档.

练习册系列答案
相关题目
9.过椭圆$\frac{{x}^{2}}{4}+{y}^{2}=1$焦点且与椭圆长轴垂直的直线与椭圆相交于A、B两点,则|AB|等于( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 1 | D. | 4$\sqrt{3}$ |
2.若函数f(x)=|mx2-(2m+1)x+m+3|恰有4个单调区间,则实数m的取值范围为( )
| A. | (-∞,$\frac{1}{8}$) | B. | (-∞,0)∪(0,$\frac{1}{8}$) | C. | (0,$\frac{1}{8}$] | D. | ($\frac{1}{8}$,1] |
3.下列命题中,命题的否定是假命题的是( )
| A. | ?x∈R,x2<x+1 | B. | ?x∈R,x2≥x+1 | ||
| C. | ?x∈R,?y∈R,xy2=y2 | D. | ?x∈R,?y∈R,x>y2 |
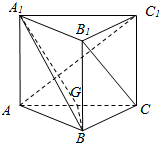 如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.
如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.