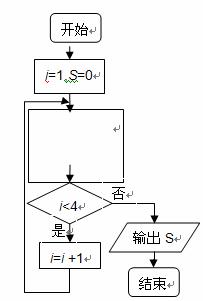
题目内容
（本小题满分10分）（1）已知数列
中，
，求数列的前
项和；
（2）已知
是等比数列
的前
项和，且公比
,
成等差数列，求证：
成等差数
列．
(1) 
(2)见解析
【解析】
试题分析：对于第一问，根据题的条件可知，数列
是以1为首项，以2为公差的等差数列，故直接应用公式即可求结果，对于第二问，根据题的条件，得出等比数列的公比所满足的关系，从而求出q的值，再得出所给的三个和分别是多少，从而得出相应的结果，即可得结论.
试题解析：（1）由已知
可得
，故数列是等差数列，且公差为2，首项为1， 3分
故
,
从而
5分
或
5分
由
成等差数列，可得
， 7分
又
,
（1） 8分
因为
，所以
（2）
把（1）式代入（2）式，得
故
成等差数列。 10分
考点：等差数列，等比数列.
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
B. 
C. 
D. 
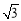，a＋b＝(
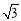，1)，则向量a＋b与向量a－b的夹角是 ．
这五个数中任取两个数，这两个数的和是奇数的概率为 ．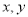
满足约束条件
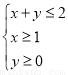,则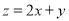
的最大值和最小值分别为（ ）
为抛物线
上一点，则抛物线焦点坐标为 ；点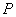
到抛物线的准线的距离为 ．