题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数且
为参数且![]() ,
,![]() ,
,![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程及
的普通方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 分别交于点
分别交于点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() :
:![]() ,
,![]() :
:![]() ;(2)
;(2)![]()
【解析】
(1)在曲线![]() 的参数方程中消去参数可得出曲线
的参数方程中消去参数可得出曲线![]() 的普通方程,在曲线
的普通方程,在曲线![]() 的极坐标方程两边同时乘以
的极坐标方程两边同时乘以![]() ,并代入
,并代入 可得出曲线
可得出曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)由曲线![]() 的参数方程得出其极坐标方程为
的参数方程得出其极坐标方程为![]() ,并设点
,并设点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 、
、![]() ,将曲线
,将曲线![]() 的极坐标方程分别代入曲线
的极坐标方程分别代入曲线![]() 、
、![]() 的表达式,求出
的表达式,求出![]() 、
、![]()
关于![]() 的表达式,然后利用三角恒等变换公式与三角函数基本性质求出
的表达式,然后利用三角恒等变换公式与三角函数基本性质求出![]() 的最大值。
的最大值。
(1)由![]() 消去参数
消去参数![]() 得
得![]() 的普通方程为:
的普通方程为:![]() ;
;
由![]() 得
得![]() ,得
,得![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,
即![]() .
.
(2)![]() 的极坐标方程为:
的极坐标方程为:![]() ,
,![]() 的极坐标方程为:
的极坐标方程为:![]()
将![]() 分别代入
分别代入![]() ,
,![]() 的极坐标方程得:
的极坐标方程得:![]() ,
,![]() ,
,
![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】一个调查学生记忆力的研究团队从某中学随机挑选100名学生进行记忆测试,通过讲解100个陌生单词后,相隔十分钟进行听写测试,间隔时间![]() (分钟)和答对人数
(分钟)和答对人数![]() 的统计表格如下:
的统计表格如下:
时间 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
答对人数 | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
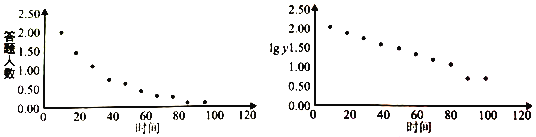
时间![]() 与答对人数
与答对人数![]() 的散点图如图:
的散点图如图:
附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对于一组数据
,对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: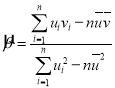 ,
,![]() .请根据表格数据回答下列问题:
.请根据表格数据回答下列问题:
(1)根据散点图判断,![]() 与
与![]() ,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果,建立![]() 与
与![]() 的回归方程;(数据保留3位有效数字)
的回归方程;(数据保留3位有效数字)
(3)根据(2)请估算要想记住![]() 的内容,至多间隔多少分钟重新记忆一遍.(参考数据:
的内容,至多间隔多少分钟重新记忆一遍.(参考数据:![]() ,
,![]() )
)
【题目】某物流公司专营从甲地到乙地的货运业务(货物全部用统一规格的包装箱包装),现统计了最近100天内每天可配送的货物量,按照可配送货物量T(单位:箱)分成了以下几组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
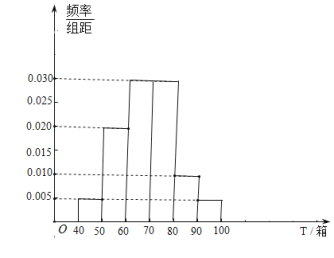
(1)该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析可配送货物量少的原因,并从这11天的数据中再抽出3天的数据进行财务分析,求这3天的数据中至少有2天的数据来自![]() 这一组的概率.
这一组的概率.
(2)由频率分布直方图可以认为,该物流公司每日的可配送货物量T(单位:箱)服从正态分布![]() ,其中
,其中![]() 近似为样本平均数.
近似为样本平均数.
(ⅰ)试利用该正态分布,估计该物流公司2000天内日货物配送量在区间![]() 内的天数(结果保留整数).
内的天数(结果保留整数).
(ⅱ)该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案.
方案一:直接发放奖金,按每日的可配送货物量划分为以下三级:![]() 时,奖励50元;
时,奖励50元;![]() ,奖励80元;
,奖励80元;![]() 时,奖励120元.
时,奖励120元.
方案二:利用抽奖的方式获得奖金,其中每日的可配送货物量不低于![]() 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于![]() 时只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为
时只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为
奖金 | 50 | 100 |
概率 |
|
|
小张恰好为该公司装卸货物的一名员工,试从数学期望的角度分析,小张选择哪种奖励方案对他更有利?
附:若![]() ,则
,则![]() ,
,![]() .
.