题目内容
若函数f（x）=
的定义域为R，则实数m的取值范围是 ．
mx2-mx+
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：题意可得，m≠0时，故
，由此求得m的范围．
|
解答：
解：由条件知：m≠0
由于关于x的不等式mx2-mx+
≥0恒成立，
∴
，
求得0＜m≤2，
故答案为：（0，2]．
由于关于x的不等式mx2-mx+
| 1 |
| m |
∴
|
求得0＜m≤2，
故答案为：（0，2]．
点评：本题主要考查二次函数的性质，函数的恒成立问题，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0）的中心为O，左焦点为F，P是双曲线上的一点
•
=0且4
•
=
2，则该双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| OP |
| PF |
| OP |
| OF |
| OF |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知{an}是等比数列，a1=1，a3=2，则a2=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
在空间直角坐标系中，点A（3，-2，4）关于xOy平面的对称点的坐标为（ ）
| A、（3，-2，4） |
| B、（3，2，4） |
| C、（-3，-2，4） |
| D、（3，-2，-4） |
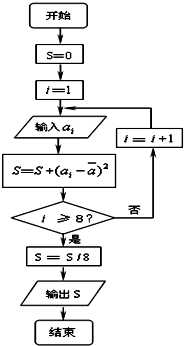对一个作直线运动的质点的运动过程观测了8次，第i次观测得到的数据为