题目内容
(文)(1)已知函数f(x)=x2+mx+3,当x∈[-2,2]时,f(x)≥m恒成立,求实数m的取值范围.(2)已知函数f(x)=x2+mx+3,当至少有一个x∈[-2,2]时,使f(x)≥m成立,求实数m的取值范围.
【答案】分析:(1)当x∈[-2,2]时,f(x)≥m恒成立等价于f(x)min≥m,按对称轴x= 与区间的位置关系分情况讨论即可求得最小值;
与区间的位置关系分情况讨论即可求得最小值;
(2)至少有一个x∈[-2,2]时,使f(x)≥m成立等价于f(x)max≥m,按 及
及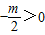 两种情况讨论即可求得最大值;
两种情况讨论即可求得最大值;
解答:解:(1)设f(x)在[-2,2]上的最小值为g(m),
则满足g(m)≥m的m即为所求.
配方得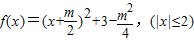 .
.
①当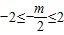 ,即-4≤m≤4时,
,即-4≤m≤4时,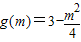 ,
,
由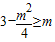 ,解得-6≤m≤2,
,解得-6≤m≤2,
所以-4≤m≤2.
②当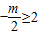 ,即m≤-4时,g(m)=f(2)=7+2m,
,即m≤-4时,g(m)=f(2)=7+2m,
由7+2m≥m,解得m≥-7,
所以-7≤m≤-4.
③当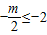 ,即m≥4时,g(m)=f(-2)=7-2m,
,即m≥4时,g(m)=f(-2)=7-2m,
由7-2m≥m,解得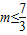 ,此与m≥4矛盾,
,此与m≥4矛盾,
故此种情况不存在.
综上所述,得-7≤m≤2.
(2)设f(x)在[-2,2]上的最大值为h(m),
则满足h(m)≥m的m即为所求.
配方得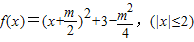 .
.
①当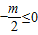 ,即m≥0时,h(m)=f(2)=7+2m,
,即m≥0时,h(m)=f(2)=7+2m,
由7+2m≥m,解得m≥-7,所以m≥0.
②当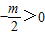 ,即m<0时,h(m)=f(-2)=7-2m,
,即m<0时,h(m)=f(-2)=7-2m,
由7-2m≥m,解得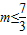 ,所以m<0.
,所以m<0.
综上所述,m的取值范围为R.
点评:本题考查不等式恒成立问题及二次函数在给定闭区间上的最值问题,恒成立问题往往转化为函数最值解决,二次函数在闭区间上的最值要利用数形结合思想、分类讨论思想解决.
 与区间的位置关系分情况讨论即可求得最小值;
与区间的位置关系分情况讨论即可求得最小值;(2)至少有一个x∈[-2,2]时,使f(x)≥m成立等价于f(x)max≥m,按
 及
及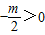 两种情况讨论即可求得最大值;
两种情况讨论即可求得最大值;解答:解:(1)设f(x)在[-2,2]上的最小值为g(m),
则满足g(m)≥m的m即为所求.
配方得
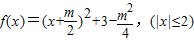 .
.①当
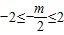 ,即-4≤m≤4时,
,即-4≤m≤4时,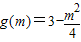 ,
,由
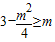 ,解得-6≤m≤2,
,解得-6≤m≤2,所以-4≤m≤2.
②当
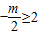 ,即m≤-4时,g(m)=f(2)=7+2m,
,即m≤-4时,g(m)=f(2)=7+2m,由7+2m≥m,解得m≥-7,
所以-7≤m≤-4.
③当
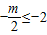 ,即m≥4时,g(m)=f(-2)=7-2m,
,即m≥4时,g(m)=f(-2)=7-2m,由7-2m≥m,解得
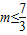 ,此与m≥4矛盾,
,此与m≥4矛盾,故此种情况不存在.
综上所述,得-7≤m≤2.
(2)设f(x)在[-2,2]上的最大值为h(m),
则满足h(m)≥m的m即为所求.
配方得
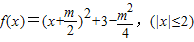 .
.①当
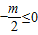 ,即m≥0时,h(m)=f(2)=7+2m,
,即m≥0时,h(m)=f(2)=7+2m,由7+2m≥m,解得m≥-7,所以m≥0.
②当
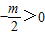 ,即m<0时,h(m)=f(-2)=7-2m,
,即m<0时,h(m)=f(-2)=7-2m,由7-2m≥m,解得
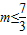 ,所以m<0.
,所以m<0.综上所述,m的取值范围为R.
点评:本题考查不等式恒成立问题及二次函数在给定闭区间上的最值问题,恒成立问题往往转化为函数最值解决,二次函数在闭区间上的最值要利用数形结合思想、分类讨论思想解决.

练习册系列答案
相关题目