题目内容
8.函数f(x)是[0,+∞)上的减函数,f(x)≠0,且 f(2)=1.证明函数F(x)=f(x)+$\frac{1}{f(x)}$在[0,2]上是减函数.分析 求导数,$F′(x)=[\frac{{f}^{2}(x)-1}{{f}^{2}(x)}]•f′(x)$,根据f(x)在(0,+∞)是减函数,且f(2)=1,可得到x∈[0,2]时,f(x)≥1,而根据f(x)是减函数,便有f′(x)<0,这样即可得出F′(x)<0,从而得出F(x)在[0,2]上是减函数.
解答 证明:$F′(x)=f′(x)-\frac{f′(x)}{{f}^{2}(x)}=[\frac{{f}^{2}(x)-1}{{f}^{2}(x)}]•f′(x)$;
∵f(x)在[0,+∞)上是减函数;
∴0≤x≤2时,f(x)≥f(2)=1;
∴f2(x)-1≥0,且f′(x)<0;
∴F′(x)<0;
∴F(x)在[0,2]上是减函数.
点评 考查函数单调性和函数导数符号的关系,减函数的定义的运用,要正确求导.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
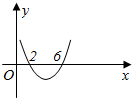 已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.
已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.