题目内容
(本题满分14分)已知函数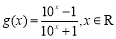 ,函数
,函数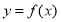 是函数
是函数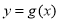 的反函数.
的反函数.
(1)求函数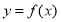 的解析式,并写出定义域
的解析式,并写出定义域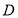 ;
;
(2) 设函数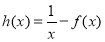 ,试判断函数
,试判断函数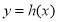 在区间
在区间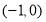 上的单调性,并说明你的理由.
上的单调性,并说明你的理由.
(1)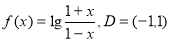 ; (2) 函数
; (2) 函数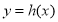 在
在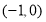 上单调递减.
上单调递减.
【解析】
试题分析:(1)先且部分分式法结合指数函数的值域求函数 的值域,即为其反函数的定义域D;再令
的值域,即为其反函数的定义域D;再令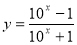 解出x然后交换x,y的位置即得函数
解出x然后交换x,y的位置即得函数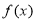 的解析式;
的解析式;
(2)先由(1)的结论可求得 的解析式和定义域,从而可判断函数
的解析式和定义域,从而可判断函数 为奇函数,从而判断函数
为奇函数,从而判断函数 在区间
在区间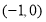 上的单调性,可转化为判断函数
上的单调性,可转化为判断函数 在区间
在区间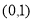 上的单调性即可.
上的单调性即可.
试题解析: (1) 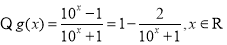 ,
,
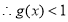 .又
.又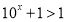 ,
,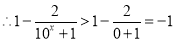 .
.
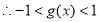 .
.
由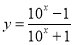 ,可解得
,可解得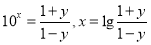 .
.
 ,
,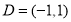 .
.
(2) 答:函数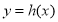 在区间
在区间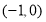 上单调递减.
上单调递减.
理由:由(1)可知,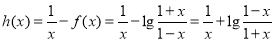 .
.
可求得函数 的定义域为
的定义域为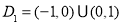 .
.
对任意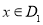 ,有
,有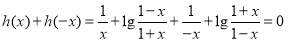 ,
,
所以,函数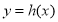 是奇函数.
是奇函数.
当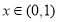 时,
时,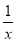 在
在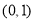 上单调递减,
上单调递减,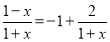 在
在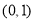 上单调递减,
上单调递减,
于是,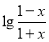 在
在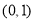 上单调递减.
上单调递减.
因此,函数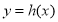 在
在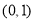 上单调递减.
上单调递减.
依据奇函数的性质,可知, 函数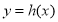 在
在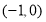 上单调递减.
上单调递减.
考点:1.反函数;2.函数的奇偶性与单调性.

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案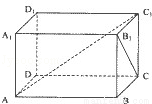
 的方程
的方程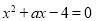 在区间
在区间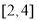 上有实数根,则实数
上有实数根,则实数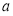 的取值范围是( )
的取值范围是( )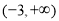 (B)
(B)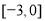 (C)
(C)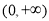 (D)
(D)
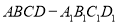 棱长为4,点
棱长为4,点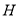 在棱
在棱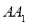 上,且
上,且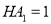 .在侧面
.在侧面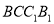 内作边长为1的正方形
内作边长为1的正方形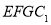 ,
,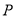 是侧面
是侧面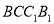 内一动点,且点
内一动点,且点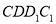 距离等于线段
距离等于线段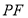 的长.则当点
的长.则当点 运动时,
运动时,  的最小值是 ( )
的最小值是 ( )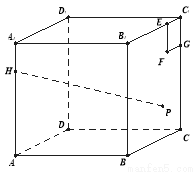
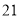 (B)
(B)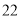 (C)
(C)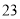 (D)
(D)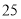
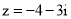 (
(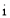 是虚数单位),则下列说法正确的是( )
是虚数单位),则下列说法正确的是( )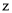 的虚部为
的虚部为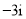
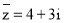
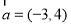 ,则下列能使
,则下列能使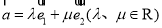 成立的一组向量
成立的一组向量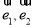 是( ).
是( ).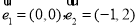
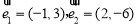
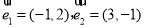
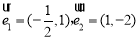
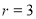 ,沿圆锥体的母线把侧面展开后得到一个圆心角为
,沿圆锥体的母线把侧面展开后得到一个圆心角为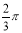 的扇形,则该圆锥体的表面积是 .
的扇形,则该圆锥体的表面积是 .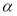 ,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).
,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).