题目内容
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,
 平面
平面 ,
,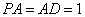 ,
, ,点
,点 是
是
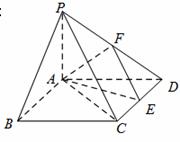 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(Ⅰ)当点 为
为 边的中点时,判断
边的中点时,判断 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)证明:无论点 在
在 边的何处,都有
边的何处,都有 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
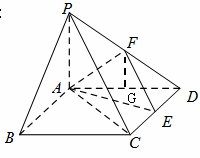 解:(Ⅰ)当点
解:(Ⅰ)当点 为
为 边的中点时,
边的中点时, 与平面
与平面 平行.
平行.
 在
在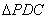 中,
中, 、
、 分别为
分别为 、
、 的中点,
的中点,

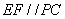 ,
,
又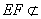 平面
平面 ,而
,而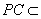 平面
平面 ,
,

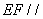 平面
平面 ;
;
(Ⅱ)证明:
 平面
平面 ,
, 平面
平面

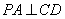

 是矩形,
是矩形,
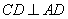

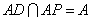 ,
,
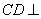 平面
平面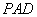
又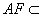 平面
平面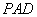

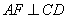
又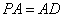 ,点
,点 是
是 中点,
中点,
 ,
,
又
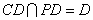

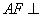 平面
平面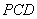 ,
,

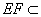 平面
平面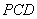 ,
,

(Ⅲ)作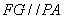 交
交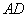 于
于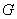 ,则
,则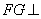 平面
平面 ,且
,且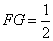 分
分
又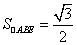

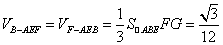 ,
,
 三棱锥
三棱锥 的体积为
的体积为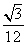 …
…

练习册系列答案
相关题目
 =__________.
=__________.
 ,若二次函数
,若二次函数 满足:①
满足:① 与
与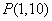 处有公共切线;②
处有公共切线;②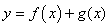 是
是 上的单调函数.则
上的单调函数.则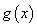 = .
= .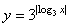 的图像是
的图像是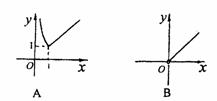
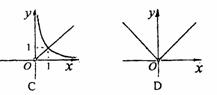
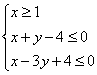 ,则目标函数
,则目标函数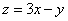 的最大值为 .
的最大值为 .  中,
中,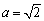 ,
, ,
, ,则A等于
,则A等于 (B)
(B) 
 (D)
(D) 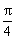 或
或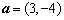 ,
,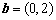 ,则向量
,则向量 在向量
在向量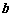 方向上的投影是 .
方向上的投影是 . 的单调递增区间是
的单调递增区间是 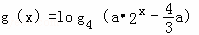 ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.