题目内容
5.已知函数$f(x)=sin(2x+\frac{π}{3}),x∈R$.(Ⅰ)在给定坐标系中,用“五点法”作出函数f(x)在一个周期上的图象(先列表,再画图);
(Ⅱ)求f(x)的对称中心;
(Ⅲ)求直线$y=\frac{1}{2}$与函数y=f(x)的图象交点的横坐标.
分析 (Ⅰ)利用“五点法”作出函数f(x)在一个周期上的图象(先列表,再画图);
(Ⅱ)根据三角函数的对称性即可求f(x)的对称中心;
(Ⅲ)根据直线$y=\frac{1}{2}$与函数y=f(x)的图象的关系解方程即可求出交点的横坐标.
解答 解:(Ⅰ)列表:
| x | $-\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| $2x+\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| f(x) | 0 | 1 | 0 | -1 | 0 |

(Ⅱ)∵y=sinx的对称中心为(kπ,0)(k∈Z),
∴由$2x+\frac{π}{3}=kπ$知:$x=\frac{kπ}{2}-\frac{π}{6}(k∈Z)$,
∴f(x)的对称中心为$(\frac{kπ}{2}-\frac{π}{6},0)(k∈Z)$
(Ⅲ)由$sin(2x+\frac{π}{3})=\frac{1}{2}$知:$2x+\frac{π}{3}=\frac{π}{6}+2kπ$或$2x+\frac{π}{3}=\frac{5π}{6}+2kπ$(k∈Z),
∴$x=-\frac{π}{12}+kπ$或$x=\frac{π}{4}+kπ(k∈Z)$
即直线$y=\frac{1}{2}$与函数y=f(x)的图象交点的横坐标为$x=-\frac{π}{12}+kπ$或$x=\frac{π}{4}+kπ(k∈Z)$
点评 本题主要考查三角函数的图象和性质,要求熟练掌握五点法作图,难度不大.

练习册系列答案
相关题目
15.顶点在原点,且过点(-1,1)的抛物线的标准方程是( )
| A. | y2=-x | B. | x2=y | C. | y2=-x或x2=y | D. | y2=x或x2=-y |
13.某学校有高一学生1200人,高二学生1000人,高三学生800人.用分层抽样的方法从中抽取150人,则抽取的高三学生、高二学生、高一学生的人数分别为( )
| A. | 60、50、40 | B. | 50、60、40 | C. | 40、50、60 | D. | 60、40、50 |
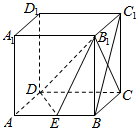 如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,
如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,