题目内容
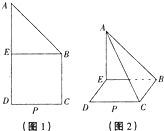 在四边形 ABC D中,BC∥AD,CD∥AD,AD=4,BC=CD=2,E、P分别为AD,CD的中点(如图1),将△ABE沿BE折 起,使二面角为A-BE-C直二面角(如图2).
在四边形 ABC D中,BC∥AD,CD∥AD,AD=4,BC=CD=2,E、P分别为AD,CD的中点(如图1),将△ABE沿BE折 起,使二面角为A-BE-C直二面角(如图2).(I)如图2,在线段AE上,是否存在一点M,使得PM∥平面ABC?若存在,请指出点M的位置,并证明你的结论,若不存在,请说明理由.
(II)如图2,若H为线段AB上的动点,当PH与平面ABE所成的角最大时,求二面角 H-PC-E的余弦值.
分析:(Ⅰ)由P是DC的中点,设想存在点M为AE中点,使PM∥平面ABC,只需取BE中点,由三角形中位线性质能够证明面面平行,从而得到线面平行;
(Ⅱ)在AB上任取一动点H,连结PH,PN,由三角形知识可知当NH垂直于AB时PH与平面ABE所成的角最大,得到H位置后可以直接找二面角 H-PC-E的平面角,然后通过解直角三角形求解二面角 H-PC-E的余弦值.
本题也可以直接建立空间直角坐标系进行求解.
(Ⅱ)在AB上任取一动点H,连结PH,PN,由三角形知识可知当NH垂直于AB时PH与平面ABE所成的角最大,得到H位置后可以直接找二面角 H-PC-E的平面角,然后通过解直角三角形求解二面角 H-PC-E的余弦值.
本题也可以直接建立空间直角坐标系进行求解.
解答:解:法一:(Ⅰ)存在点M,当M为线段AE的中点时,PM∥平面BCA.

事实上,取EB的中点N,连接PN,MN,则MN∥BA,PN∥CB,
所以平面PMN∥平面ABC,
因为PM在平面PMN内,
所以PM∥平面ABC.
(Ⅱ)如图,

连接PH,NH,可知PN⊥平面ABE,
所以PH与平面ABE所成角为∠PHN,
又tan∠PHN=
,PN=2,
所以当NH⊥AB时,PH与平面ABE所成角最大,
可得BH=
,
过H作HR⊥EB交EB于R,
则HR⊥平面BCDE,且BR=HR=
,
过R做RG⊥CD垂足为G,连接HG,
则HG⊥CD,
所以∠GHR为二面角H-PC-E的平面角,
所以在直角△HRG中tan∠HGR=
=
,
所以cos∠HGR=
,所以二面角H-PC-E的余弦值为
.
法二:(Ⅰ)存在点M,当M为线段AE的中点时,PM∥平面BCA,
建立如图所示空间直角坐标系,

则A(0,0,2),M(0,0,1),P(2,1,0),B(0,2,0),C(2,2,0),
AB中点F(0,1,1),
所以
=(-2,-1,1),
=(2,0,0),
=(0,2,-2),
=(0,1,1).
可知
•
=0,
•
=0,∴EF⊥平面ABC,
又
•
=0,
∴PM∥平面ABC.
(Ⅱ) 可知P ( 2,1,0 ),A(0,0,2),E(0,0,0),B(0,2,0),
设H(x,y,z),则
=(0,-2,2),
=(x,y-2,z),
设
=λ
,则得H(0,2-2λ,2λ),
所以
=(-2,1-2λ,2λ),因为点P到平面ABE的距离为定值2,
所以当PH最小时PH与平面ABE所成角最大,
此时
⊥
,即
•
=0,得λ=
,所以H(0,
,
),
所以
=(0,-
,
),
设平面PCH的一个法向量为
=(x,y,z),
=(0,1,0),
=(-2,
,
)
则由
,可得
,则
=(
,0,2),
平面PBE的一个法向量为
=(0,0,2),
设二面角H-PC-E的大小为θ,
则cosθ=
=
.

事实上,取EB的中点N,连接PN,MN,则MN∥BA,PN∥CB,
所以平面PMN∥平面ABC,
因为PM在平面PMN内,
所以PM∥平面ABC.
(Ⅱ)如图,

连接PH,NH,可知PN⊥平面ABE,
所以PH与平面ABE所成角为∠PHN,
又tan∠PHN=
| PN |
| NH |
所以当NH⊥AB时,PH与平面ABE所成角最大,
可得BH=
| ||
| 2 |
过H作HR⊥EB交EB于R,
则HR⊥平面BCDE,且BR=HR=
| 1 |
| 2 |
过R做RG⊥CD垂足为G,连接HG,
则HG⊥CD,
所以∠GHR为二面角H-PC-E的平面角,
所以在直角△HRG中tan∠HGR=
| HR |
| RG |
| 1 |
| 4 |
所以cos∠HGR=
4
| ||
| 17 |
4
| ||
| 17 |
法二:(Ⅰ)存在点M,当M为线段AE的中点时,PM∥平面BCA,
建立如图所示空间直角坐标系,

则A(0,0,2),M(0,0,1),P(2,1,0),B(0,2,0),C(2,2,0),
AB中点F(0,1,1),
所以
| PM |
| BC |
| AB |
| EF |
可知
| EF |
| BC |
| EF |
| AB |
又
| EF |
| PM |
∴PM∥平面ABC.
(Ⅱ) 可知P ( 2,1,0 ),A(0,0,2),E(0,0,0),B(0,2,0),
设H(x,y,z),则
| BA |
| BH |
设
| BH |
| BA |
所以
| PH |
所以当PH最小时PH与平面ABE所成角最大,
此时
| PH |
| BA |
| PH |
| BA |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
所以
| BH |
| 1 |
| 2 |
| 1 |
| 2 |
设平面PCH的一个法向量为
| n |
| PC |
| PH |
| 1 |
| 2 |
| 1 |
| 2 |
则由
|
|
| n |
| 1 |
| 2 |
平面PBE的一个法向量为
| EA |
设二面角H-PC-E的大小为θ,
则cosθ=
| ||||
|
|
4
| ||
| 17 |
点评:本题考查了线面平行的判定,解答时常借助于三角形的中位线证明,考查了二面角的平面角的求法,常用“寻找垂面,构造垂线”法寻找二面角的平面角,考查了利用空间向量证明线面平行及利用空间向量求解二面角的大小,关键是建立正确的空间右手系,是中档题.

练习册系列答案
相关题目

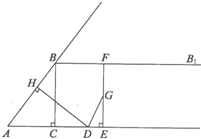 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒. 某小区有一块三角形空地,如图△ABC,其中AC=180米,BC=90米,∠C=90°,开发商计划在这片空地上进行绿化和修建运动场所,在△ABC内的P点处有一服务站(其大小可忽略不计),开发商打算在AC边上选一点D,然后过点P和点D画一分界线与边AB相交于点E,在△ADE区域内绿化,在四边形BCDE区域内修建运动场所.现已知点P处的服务站与AC距离为10米,与BC距离为100米.设DC=d米,试问d取何值时,运动场所面积最大?
某小区有一块三角形空地,如图△ABC,其中AC=180米,BC=90米,∠C=90°,开发商计划在这片空地上进行绿化和修建运动场所,在△ABC内的P点处有一服务站(其大小可忽略不计),开发商打算在AC边上选一点D,然后过点P和点D画一分界线与边AB相交于点E,在△ADE区域内绿化,在四边形BCDE区域内修建运动场所.现已知点P处的服务站与AC距离为10米,与BC距离为100米.设DC=d米,试问d取何值时,运动场所面积最大?