题目内容
 某小区有一块三角形空地,如图△ABC,其中AC=180米,BC=90米,∠C=90°,开发商计划在这片空地上进行绿化和修建运动场所,在△ABC内的P点处有一服务站(其大小可忽略不计),开发商打算在AC边上选一点D,然后过点P和点D画一分界线与边AB相交于点E,在△ADE区域内绿化,在四边形BCDE区域内修建运动场所.现已知点P处的服务站与AC距离为10米,与BC距离为100米.设DC=d米,试问d取何值时,运动场所面积最大?
某小区有一块三角形空地,如图△ABC,其中AC=180米,BC=90米,∠C=90°,开发商计划在这片空地上进行绿化和修建运动场所,在△ABC内的P点处有一服务站(其大小可忽略不计),开发商打算在AC边上选一点D,然后过点P和点D画一分界线与边AB相交于点E,在△ADE区域内绿化,在四边形BCDE区域内修建运动场所.现已知点P处的服务站与AC距离为10米,与BC距离为100米.设DC=d米,试问d取何值时,运动场所面积最大?分析:解法一:以C为坐标原点,CB所在直线为x轴,CA所在直线为y轴建立直角坐标系,得到C、A、B、P、D的坐标,再写出直线DE、AB的方程,由此联立解出E的坐标,进而表示△ADE的面积,利用基本不等式的知识分析可得答案;
解法二:分别过点P,E作AC的垂线,垂足为Q,F,设EF=h,分情况讨论可得EF的长度,进而可以表示△ADE的面积,再利用基本不等式的知识分析可得答案.
解法二:分别过点P,E作AC的垂线,垂足为Q,F,设EF=h,分情况讨论可得EF的长度,进而可以表示△ADE的面积,再利用基本不等式的知识分析可得答案.
解答: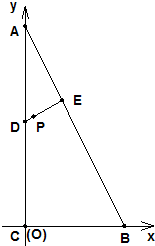 解:法一:以C为坐标原点,CB所在直线为x轴,CA所在直线为y轴建立直角坐标系,
解:法一:以C为坐标原点,CB所在直线为x轴,CA所在直线为y轴建立直角坐标系,
则C(0,0),A(0,180),B(90,0),P(10,100),D(0,d).
DE直线方程:y-100=
(x-10),①
AB所在直线方程为2x+y=180,②
解①、②组成的方程组得,xE=
,
∵直线DE经过点B时d=
,
∴0<d<
,
S△ADE=
AD•|xE|=
•(180-d)•
设120-d=t∈(
,120),S△ADE=5•
=5•(t+
+120),
∵t+
≥120(当且仅当t=60,即k=4时取等号),
此时d=120-t=60,
∴当d=60时,绿化面积最小,从而运动区域面积最大.
法二:如图,分别过点P,E作AC的垂线,垂足为Q,F,设EF=h,
若如图1所示,则PQ=10,CQ=100,DQ=100-d,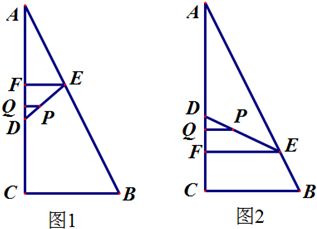
由△AFE~△ACB得
=
,即AF=2h,从而CF=180-2h,DF=180-2h-d,
由△DPQ~△DEF得
=
,解得h=
若如图2所示,则PQ=10,CQ=100,DQ=d-100,AF=2h,CF=180-2h,DF=2h+d-180,由△DPQ~△DEF得
=
,
解得h=
;
由0<h<90得0<d<
,
由S△ADE=
AD•h=
•(180-d)•
,
设120-d=t∈(
,120),
S△ADE=5•
=5•(t+
+120),
∵t+
≥120(当且仅当t=60,即k=4时取等号),
此时d=120-t=60,
∴当d=60时,绿化面积最小,从而运动区域面积最大.
 解:法一:以C为坐标原点,CB所在直线为x轴,CA所在直线为y轴建立直角坐标系,
解:法一:以C为坐标原点,CB所在直线为x轴,CA所在直线为y轴建立直角坐标系,则C(0,0),A(0,180),B(90,0),P(10,100),D(0,d).
DE直线方程:y-100=
| d-100 |
| -10 |
AB所在直线方程为2x+y=180,②
解①、②组成的方程组得,xE=
| 10d-1800 |
| d-120 |
∵直线DE经过点B时d=
| 225 |
| 2 |
∴0<d<
| 225 |
| 2 |
S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 10d-1800 |
| d-120 |
设120-d=t∈(
| 15 |
| 2 |
| (60+t)2 |
| t |
| 3600 |
| t |
∵t+
| 3600 |
| t |
此时d=120-t=60,
∴当d=60时,绿化面积最小,从而运动区域面积最大.
法二:如图,分别过点P,E作AC的垂线,垂足为Q,F,设EF=h,
若如图1所示,则PQ=10,CQ=100,DQ=100-d,

由△AFE~△ACB得
| AF |
| 180 |
| h |
| 90 |
由△DPQ~△DEF得
| 10 |
| h |
| 100-d |
| 180-2h-d |
| 1800-10d |
| 120-d |
若如图2所示,则PQ=10,CQ=100,DQ=d-100,AF=2h,CF=180-2h,DF=2h+d-180,由△DPQ~△DEF得
| 10 |
| h |
| 100-d |
| 180-2h-d |
解得h=
| 1800-10d |
| 120-d |
由0<h<90得0<d<
| 225 |
| 2 |
由S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 10d-1800 |
| d-120 |
设120-d=t∈(
| 15 |
| 2 |
S△ADE=5•
| (60+t)2 |
| t |
| 3600 |
| t |
∵t+
| 3600 |
| t |
此时d=120-t=60,
∴当d=60时,绿化面积最小,从而运动区域面积最大.
点评:本题考查基本不等式的应用,关键是根据题意,建立正确的模型,得到关于关于三角形面积的不等关系式.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 (2013•上海)如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积.
(2013•上海)如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积. 如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积.
如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积.