题目内容
设
，若
和
的等差中项是
，则
的最小值是（ ）
| A．1 | B．2 | C．4 | D． |
B
解析试题分析：因为和的等差中项是，所以
，所以
，当且仅当
时取等号.
考点：本小题主要考查对数的运算和等差中项的应用以及应用基本不等式求最值.
点评：应用基本不等式求最值时，一定要注意一正二定三相等三个条件缺一不可.
练习册系列答案
相关题目
若
( )
A． | B． | C． | D． |
若
且满足
，则
的最小值是（ ）
A． | B． | C．7 | D．6 |
若
且2
=2，则
的最小值是（ ）
| A．2 | B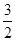． | C． | D． |
下列函数中，最小值是4的函数是( )
A． | B． ( ) |
C． | D． |
已知
，
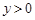，且
，则
的最小值是 （ ）
A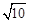． | B． | C． | D． |
若点
在第一象限且在
上移动，则
（ ）
| A．最大值为1 | B．最小值为1 | C．最大值为2 | D．没有最大、小值 |
△ABC满足
，∠BAC=30°，设M是△ABC内的一点(不在边界上)，定义f(M)=(x,y,z)，其中
分别表示△MBC，△MCA,△MAB的面积，若
，则
的最小值为__________________
若
，则下列不等式成立的是
A． | B． |
C． | D． |