题目内容
Sn是数列{an}的前n项和,则“Sn是关于n的二次函数”是“数列{an}为等差数列”的
- A.充分不必要条件
- B.必要不充分条件
- C.充分必要条件
- D.既不充分也不必要条件
D
分析:利用必要条件、充分条件与充要条件的概念及等差数列的性质可得“Sn是关于n的二次函数”不能?“数列{an}为等差数列”,反之亦然,从而可得答案.
解答:不妨设Sn=n2-1,
则当n=1时,a1=S1=0,
当n≥2时,an=Sn-Sn-1=2n-1,
显然,当n=1时,a1=0≠1,
∴an=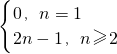 ,即数列{an}不是等差数列,
,即数列{an}不是等差数列,
也就是说,“Sn是关于n的二次函数”不能?“数列{an}为等差数列”,充分性不成立;
反之,“数列{an}为等差数列”,不妨取an=0,
则Sn=na1=0,Sn不是关于n的二次函数,即必要性不成立,
故选D.
点评:本题考查等差数列的性质,考查必要条件、充分条件与充要条件的概念,考查理解与推理能力,考查特值法在选择题中的应用,属于中档题.
分析:利用必要条件、充分条件与充要条件的概念及等差数列的性质可得“Sn是关于n的二次函数”不能?“数列{an}为等差数列”,反之亦然,从而可得答案.
解答:不妨设Sn=n2-1,
则当n=1时,a1=S1=0,
当n≥2时,an=Sn-Sn-1=2n-1,
显然,当n=1时,a1=0≠1,
∴an=
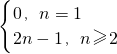 ,即数列{an}不是等差数列,
,即数列{an}不是等差数列,也就是说,“Sn是关于n的二次函数”不能?“数列{an}为等差数列”,充分性不成立;
反之,“数列{an}为等差数列”,不妨取an=0,
则Sn=na1=0,Sn不是关于n的二次函数,即必要性不成立,
故选D.
点评:本题考查等差数列的性质,考查必要条件、充分条件与充要条件的概念,考查理解与推理能力,考查特值法在选择题中的应用,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目