题目内容
1.在(2+$\sqrt{x}$-$\frac{1}{{x}^{2006}}$)10的展开式中,x4项的系数为180.分析 (2+$\sqrt{x}$-$\frac{1}{{x}^{2006}}$)10的展开式中,Tr+1=${∁}_{10}^{r}$$(2+\sqrt{x})^{r}(-\frac{1}{{x}^{2006}})^{10-r}$,必须10-r=0,解得r=10.T11=${∁}_{10}^{10}$$(2+\sqrt{x})^{10}$,再利用$(2+\sqrt{x})^{10}$的通项公式即可得出.
解答 解:(2+$\sqrt{x}$-$\frac{1}{{x}^{2006}}$)10的展开式中,Tr+1=${∁}_{10}^{r}$$(2+\sqrt{x})^{r}(-\frac{1}{{x}^{2006}})^{10-r}$,
必须10-r=0,解得r=10.
∴T11=${∁}_{10}^{10}$$(2+\sqrt{x})^{10}$,
$(2+\sqrt{x})^{10}$的通项公式Tk+1=${∁}_{10}^{k}{2}^{10-k}(\sqrt{x})^{k}$=210-k${∁}_{10}^{k}$${x}^{\frac{k}{2}}$,
令$\frac{k}{2}$=4,解得k=8.
∴在(2+$\sqrt{x}$-$\frac{1}{{x}^{2006}}$)10的展开式中,x4项的系数为1×${2}^{2}{∁}_{10}^{8}$=180
故答案为:180.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.设抛物线C:x2=4y的焦点为F,斜率为k的直线l经过点F,若抛物线C上存在四个点到直线l的距离为2,则k的取值范围是( )
| A. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | B. | (-$\sqrt{3}$,-1)∪(1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-∞,-1)∪(1,+∞) |
9.设x,y满足约束条件$\left\{\begin{array}{l}{x≤0}\\{2x+y≥1}\\{x+y≤2}\end{array}\right.$,则z=3x+y的最小值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.四条直线每两条都相交,且任三条都不交于一点,它们可确定的平面个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.若$\frac{sinα+cosα}{cosα-sinα}$=tanβ,α,β∈[0,$\frac{π}{2}$),则β-α等于( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
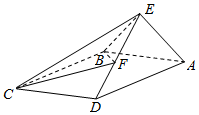 如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.
如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.