题目内容
(Ⅰ)设a>0且a≠1,求函数f(x)=(Ⅱ)设x、y均为正实数,证明不等式:(x+y)ln![]() ≤xlnx+ylny.
≤xlnx+ylny.
解:(Ⅰ)解法一:
因为ax>0,a>0,所以![]() 中
中
当且仅当ax=a,即x=1时,上式等号成立,
所以f(x)≥0对任意的x∈![]() 恒成立,
恒成立,
所以,当且仅当x=1时,f(x)取最小值
解法二:
![]() (x)=
(x)=![]()
当x>1时,x>![]() 成立
成立
若a>1,则lna>0,ax-![]() >0;
>0;
若0<a<1,则lna<0,ax-![]() <0.所以
<0.所以![]() (x)>0
(x)>0
即函数f(x)在(1,+∞)上单调递增
又f(1)=0, 所以[f(x)]min=f(1)=0.
(Ⅱ)证明:
①当x=y时,(x+y)ln![]() =xlnx+ylny
=xlnx+ylny
②当x≠y时,不失一般性,设x>y>0并取y=m,则x∈(m,+∞).
设g(x)=xlnx+ylny-(x+y)ln![]()
即g(x)=xlnx-(x+m)ln![]() +mlnm,x∈(m,+∞)
+mlnm,x∈(m,+∞)
![]() (x)=lnx+1-(ln
(x)=lnx+1-(ln![]() +
+![]() ·
·![]() )
)
=lnx-ln![]() =ln
=ln![]()
因为2x>x+m>0 所以![]() >1
>1
所以![]() (x)=ln
(x)=ln![]() >0
>0
所以g(x)在(m,+∞)上单调递增
又g(m)=0
所以g(x)>0,即xlnx-(x+m)ln![]() +mlnm>0
+mlnm>0
所以(x+m)ln![]() <xlnx+mlnm
<xlnx+mlnm
即(x+y)ln![]() <xlnx+ylny.
<xlnx+ylny.
综合①,②,有不等式
(x+y)ln![]() ≤xlnx+ylny成立
≤xlnx+ylny成立

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
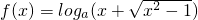 (x≥1)
(x≥1)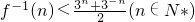 ,求a的取值范围.
,求a的取值范围. (x≥1)
(x≥1)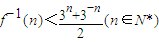 ,求a的取值范围.
,求a的取值范围.