题目内容
数列
,
,…
的前n项和为( )
| 1 |
| 1+2 |
| 1 |
| 1+2+3 |
| 1 |
| 1+2+…+n |
A.
| B.
| C.
| D.
|
由数列可知数列的通项公式an=
=
=
=2(
-
),
∴数列的前n项和S=2(
-
+
-
+…+
-
)=2(
-
)=
,
故选:C.
| 1 |
| 1+2+…+(n+1) |
| 1 | ||
|
| 2 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴数列的前n项和S=2(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| n+2 |
故选:C.

练习册系列答案
相关题目


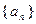 的首项
的首项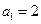 ,公比
,公比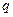 是最小的正整数,则数列
是最小的正整数,则数列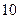 项的和为
项的和为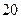 B
B 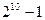 C
C 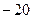 D
D