题目内容
已知数列{an}的各项均是正数,其前n项和为Sn,满足Sn=4-an.
(1)求数列{an}的通项公式;
(2)设bn=
(n∈N*),数列{bnbn+2}的前n项和为Tn,求证:Tn<
.
(1)求数列{an}的通项公式;
(2)设bn=
| 1 |
| 2-log2an |
| 3 |
| 4 |
(1)由Sn=4-an.得S1=4-a1,解得a1=2,
而an+1=Sn+1-Sn=(4-an+1)-(4-an)=an-an+1,即2an+1=an,
∴
=
,
可见,数列{an}是首项为2,公比为
的等比数列.
∴an=2•(
)n-1=(
)n-2;
(2)证明:∵bn=
=
=
,
∴bnbn+2=
=
(
-
),
∴数列{bnbn+2}的前n项和
Tn=
[(1-
)+(
-
)+(
-
)+(
-
)+…+(
-
)+(
-
)+(
-
)]
=
(1+
-
-
)
=
(
-
-
)=
-
(
+
)<
.
而an+1=Sn+1-Sn=(4-an+1)-(4-an)=an-an+1,即2an+1=an,
∴
| an+1 |
| an |
| 1 |
| 2 |
可见,数列{an}是首项为2,公比为
| 1 |
| 2 |
∴an=2•(
| 1 |
| 2 |
| 1 |
| 2 |
(2)证明:∵bn=
| 1 |
| 2-log2an |
| 1 |
| 2-(2-n) |
| 1 |
| n |
∴bnbn+2=
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴数列{bnbn+2}的前n项和
Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| n-2 |
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
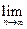
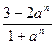 的值是 .
的值是 .