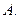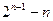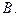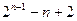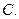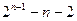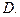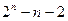题目内容

如图，在面积为1的正△A1B1C1内作正△A2B2C2，使
A1A2
=2
A2B1
，
B1B2
=2
B2C1
，
C1C2
=2
C2A1
，依此类推，在正△A2B2C2内再作正△A3B3C3，…．记正△AiBiCi的面积为ai（i=1，2，…，n），则a1+a2+…+an=______．
由
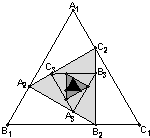
A1A2
=2
A2B1
，
B1B2
=2
B2C1
，
C1C2
=2
C2A1
，可得S2=
1
3
S1
依此类推可得所作三角形的面积构成以1为 项，以
1
3
为公比的等比数列
∴a1+a2+…+an=
1-(
1
3
)n
1-
1
3
=
3
2
(1-
1
3n
)
故答案为：
3
2
(1-
1
3n
)
练习册系列答案
相关题目
已知递增的等比数列{an}的前三项之积为512，且这三项分别依次减去1、3、9后又成等差数列．
（1）求数列{an}的通项公式；
（2）若Tn=
1
a1
+
2
a2
+
3
a3
+…+
n
an
，求Tn．
数列{an}是等差数列，Sn是前n项和，a4=3，S5=25
（1）求数列{an}的通项公式an．
（2）设bn=|an|，求b1+b2+…+bn．
数列
1
1+2
，
1
1+2+3
，…
1
1+2+…+n
的前n项和为（　　）
A．
n
n+1
B．
2n
n+1
C．
n
n+2
D．
n
2(n+1)
已知数列{an}是一个等差数列，且a2=5，a5=11．
（Ⅰ）求数列{an}的通项公式an；
（Ⅱ）令bn=
1
a2n
-1
(n∈N*)，求数列{bn}的前n项和Tn．
在数列{an}中，a1=-6×210，点（n，2a+1-an）在直线y=211x上，设bn=an+1-an+t，数列{bn}是等比数列．
（1）求出实数t；（2）令cn=|log2bn|，问从第几项开始，数列{cn}中连续20项之和为100？
根据程序框图，将输出的x，y值依次分别记为x1，x2，…，x2013；y1，y2，…，y2013
（Ⅰ）写出数列{xn}的递推公式，求{xn}的通项公式；
（Ⅱ）写出数列{yn}的递推公式，求{yn}的通项公式；
（Ⅲ）求数列{xn+yn}的前n项和Sn（n≤2013）．
已知不等式x2-2x-3＜0的整数解由小到大构成数列{an}前三项，若数列{an+2a2}的前n项和为Sn，则Sn=______．
的结果为(    )
            

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网