题目内容
6.设a∈R,A={x|x∈R,|x-a|≤1},B={x|x∈R,|x-1|≤a2},若A不是B的真子集,求a的取值范围.分析 化简集合A,B,求出A是B的真子集时a的范围,即可求出A不是B的真子集时a的取值范围.
解答 解:A={x|x∈R,|x-a|≤1}=[a-1,a+1],B={x|x∈R,|x-1|≤a2}=[1-a2,1+a2],
若A是B的真子集,则1-a2≤a-1,a+1≤1+a2,∴a≤-2或a≥1,
∵A不是B的真子集,
∴-2<a<1.
点评 本题考查集合的关系,考查补集思想,比较基础.

练习册系列答案
相关题目
17.下列求导数运算正确的是( )
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{x^{2}}$ | B. | (log2x)′=$\frac{1}{xln2}$ | C. | (3x)′=3xlog3e | D. | (x2)′=-2x |
1.函数y=sin2x的图象在点A($\frac{π}{6}$,$\frac{1}{4}$)处的切线的斜率是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
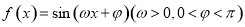 ,直线
,直线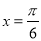 是它的一条对称轴,且
是它的一条对称轴,且 是离该轴最近的一个对称中心,则
是离该轴最近的一个对称中心,则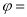 ( )
( )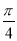 B.
B.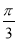 C.
C.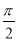 D.
D.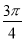
 ,若
,若 ,则
,则 ( )
( ) B.
B. C.-1 D.1
C.-1 D.1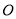 的半径为1,
的半径为1,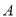 是圆上的定点,
是圆上的定点,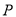 是圆上的动点,角
是圆上的动点,角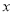 的始边为射线
的始边为射线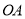 ,终边为射线
,终边为射线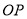 ,过点
,过点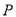 作直线
作直线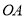 的垂线,垂足为
的垂线,垂足为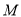 ,将点
,将点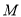 到直线
到直线 的距离与
的距离与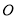 到
到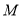 的距离之和表示成
的距离之和表示成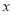 的函数
的函数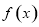 ,则
,则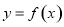 在
在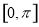 上的图象大致是( )
上的图象大致是( )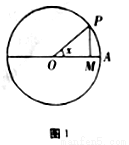
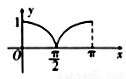 B.
B.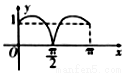
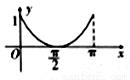 D.
D.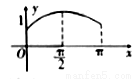
 分别与曲线
分别与曲线 交于点
交于点 ,则
,则 的最小值为( )
的最小值为( ) C.1 D.
C.1 D.