题目内容
设x1,x2,x3, …,xn都是正实数，且x1+x2+x3+…+xn=S.求证：
.
证法一：根据柯西不等式，得
左边=
=［(S-x1)+(S-x2)+ …+(S-xn)］×
≥
=
(x1+x2+…+xn)2=
×S2=
=右边.
∴原不等式成立.
证法二：∵a∈R+，则a+
≥2.
∴a≥2-
.
∴
.
n个式子相加，有
=
.∴原不等式成立.
证法三：
(S-xi)≥
.
∴
,
∴
.
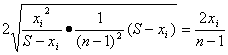∴原不等式成立.
练习册系列答案
阅读快车系列答案
相关题目
+
+
)≥9.
+
+
)≥9.
+
+
)≥9.